What if I told you that the security of your online communications hinges on a complex mathematical puzzle? Imagine trying to send a secret message to a friend, but only your friend can read it, even if the entire world has access to it. This is the essence of RSA key encryption and decryption, a cornerstone in the realm of cryptography that enables secure communications in our digital age.
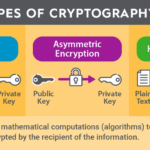
At its core, RSA (Rivest-Shamir-Adleman) is an asymmetric encryption algorithm that uses a pair of keys for the encryption and decryption processes. Asymmetric means that two different keys perform these tasks: a public key is used for encryption, while a private key, known only to the recipient, is employed for decryption. This key pair creates a formidable barrier against unauthorized access, but how does it work in practice?
The RSA algorithm begins with the generation of two distinct prime numbers, typically denoted as p and q. The security of RSA relies fundamentally on the properties of these primes, particularly their difficulty in being factored. Once selected, these primes are multiplied together to produce n, which forms part of both the public and private keys.
Now, here arises an intriguing dilemma: How are these keys derived and what role does mathematical ingenuity play in this process? To generate a public key, the next step involves determining an integer e, which is coprime to (p-1)(q-1). Essentially, e is chosen such that it shares no common factors with the totient function of n, ensuring a wide variety of potential values that do not compromise the system’s integrity. Commonly, e is selected as 65537 due to its mathematical properties, which optimize the encryption process.
The public key becomes a duo, comprising the values (n, e). This pair is disseminated widely, allowing anyone to encrypt messages intended for the owner of the private key. However, the private key, which consists of the integer d, remains confidential. The value d is computed using the modular multiplicative inverse of e modulo (p-1)(q-1). This might sound perplexing, but the crux of it is that d enables the decryption of messages, transforming the cryptic into the comprehensible.
Upon receiving an encrypted message, the recipient leverages their private key d to decipher it. This decryption process exemplifies the brilliance of RSA. Mathematically, a personalized message m, when encrypted, appears as c = m^e mod n. Conversely, the decryption process entails calculating m = c^d mod n. Here, the interplay between modular arithmetic and exponentiation illuminates the strength of RSA encryption, making it robust against a myriad of cryptanalytic attacks.
Consider a playful conundrum: If RSA relies on the difficulty of factoring large numbers, what happens when computational technology advances? The advent of quantum computers introduces a potential challenge, as algorithms such as Shor’s algorithm could factor large integers significantly faster than classical computers. This foreshadows an impending era of cryptographic upheaval, inciting a vital discussion on the evolution and adaptability of encryption systems.
Despite this looming uncertainty, RSA encryption endures as an emblem of security. It underpins various applications, from securing emails and online transactions to enabling secure connections through SSL/TLS. Not only does RSA provide confidentiality, but it also authenticates the source of messages, ensuring integrity and trust in electronic communications.
As one delves deeper into RSA, the implications of key management and longevity arise. The longevity of cryptographic keys poses another varied puzzle; keys must be regularly rotated to effectively mitigate risks. Additionally, the size of the keys themselves can significantly influence security: longer keys enhance security at the cost of computational efficiency. Current recommendations often suggest a minimum of 2048-bit keys, a standard that continues to evolve with the pace of computing power advancements.
Moreover, the implementation of RSA in real-world applications requires meticulous care. Trade-offs between security and performance must be assessed, as overly ambitious key sizes can lead to inefficiencies. Furthermore, vulnerabilities may arise not solely from the algorithm itself but also from implementation flaws, making rigorous testing and adherence to best practices paramount.
In summation, RSA key encryption and decryption embody a fascinating interplay of mathematics, security, and practicality. The sheer elegance of its design coupled with its crucial role in safeguarding information cannot be overstated. As we traverse the digital landscape, the significance of cryptographic measures like RSA becomes increasingly pronounced, ultimately shaping the future of our communications.
In conclusion, RSA serves not only as a bastion of data security but also as a reminder of the intricate relationship between innovation and vulnerability. How prepared are we for the next paradigm shift in encryption? Stay vigilant, for the world of cryptography never sleeps, constantly adapting to both threats and advancements.






Leave a Comment