The domain of cryptography is often likened to a sophisticated chess game played between two adversaries: those who seek to protect information and those who endeavor to undermine that protection. Among the stratagems employed in this ongoing contest is RSA, an acronym for Rivest-Shamir-Adleman, the names of its architects. RSA stands as a paragon of public-key cryptography, transforming the notion of secure communication into a tangible reality.
At its core, RSA is founded upon the principles of number theory, particularly the properties of prime numbers. Consider prime numbers as the building blocks of all integers, akin to elemental particles in a vast cosmic universe. They are indivisible by any other numbers except for one and themselves, rendering them exceedingly valuable in the cryptographic arena. In the grand tapestry of digital security, RSA weaves a unique narrative by relying on the multiplication and factorization of these prime numbers.
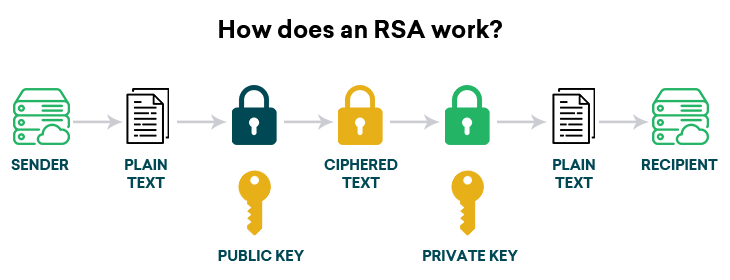
To elucidate the workings of RSA, envision a scenario involving a locked box. This box can be locked with a padlock that only the owner possesses. Anyone can place an item in the box, secure it, and send it to the owner, but only the owner can unlock the box and retrieve the contents. In RSA, this interplay of locking and unlocking symbolizes how public and private keys function. The public key serves as the padlock, widely disseminated, while the private key is the exclusive key that opens the lock.
The RSA algorithm initiates its journey by selecting two large prime numbers, let’s denote them as p and q. The product of these two primes forms the modulus n, which is foundational to the encryption and decryption process. The security of RSA hinges upon the difficulty of factoring the product of two large primes, a problem that remains computationally strenuous even with today’s advanced algorithms and hardware.
Next comes the selection of an exponent e, which must be coprime to (p-1)(q-1). This plays a crucial role in defining the relationship between the keys. The final step is computing the private exponent d, which is the modular multiplicative inverse of e. This approach establishes an intricate dance between the keys; the public key (n, e) allows others to encrypt messages, whereas the private key d enables the decryption of these messages.
So, why has RSA withstood the test of time and remained a stalwart in secure communications? Let’s delve deeper into the metaphorical magic that RSA conjures, illuminating its enduring appeal.
Firstly, security through obscurity is a fallacy in cryptography. RSA, however, thrives on the principle of transparency. Its algorithm is publicly known and widely scrutinized, yet this very exposure contributes to its robustness. The strength of RSA lies not in concealment but in the mathematical foundation that governs it—a foundation that has been thoroughly examined, debated, and refined over decades.
Furthermore, RSA embodies a unique juxtaposition of simplicity and complexity. The underlying mathematics may appear to be an intricate web of numbers and computations, yet the operational mechanics for users are elegantly simple. Generating keys can be streamlined into a process that is accessible even to non-experts, making RSA a go-to choice for securing information without necessitating a deep dive into cryptographic principles.
RSA possesses another layer of elegance through its scalability. As the complexity of the problem increases—specifically, the size of the prime numbers involved—the difficulty of cracking the encryption scales exponentially. In an era where computational power has surged, using sufficiently large keys (2048 bits and beyond) ensures that the time required to break RSA encryption remains impractically prohibitive for potential attackers.
Additionally, RSA integrates seamlessly into broader cryptographic frameworks, empowering TLS/SSL protocols that underpin secure web browsing—a cornerstone of online safety. This interoperability magnifies its significance, allowing it to coexist and complement other cryptographic protocols such as symmetric encryption, which is faster yet requires the establishment of a shared secret key.
As society veers toward an increasingly interconnected digital landscape, the need for secure communications becomes ever more paramount. RSA’s historical significance, combined with its pragmatic adaptability, positions it as a stalwart defender of data integrity in transit. It embodies a timeless cipher whose secrets are both complex and securely grounded in mathematical reality.
Nevertheless, it is essential to acknowledge that no cryptographic algorithm exists in a vacuum. The emergence of quantum computing looms on the horizon, potentially threatening RSA’s long-standing dominion. Quantum algorithms, particularly Shor’s algorithm, could unravel RSA’s resilience by efficiently factoring large integers. Consequently, the cryptographic community is already investigating post-quantum algorithms that may supplant RSA and safeguard information in a futuristic paradigm.
As advancements in technology march forward, the cryptographic terrain continually evolves. RSA’s fundamental principles, however, remind us that robust security is not merely about the complexity of algorithms but also the steadfastness of mathematical foundations. Ultimately, in the arena of cryptography, RSA stands as a robust guardian; a centuries-old solution poised to adapt and thrive amid the challenges of tomorrow.






Leave a Comment