Elliptic Curve Digital Signature Algorithm (ECDSA) is a cryptographic framework at the bedrock of contemporary digital security, particularly in the realm of cryptocurrencies. Our exploration of ECDSA will unravel how it adeptly generates public keys with precision, while ensuring the integrity and authenticity of digital communications. As we embark on this journey, consider this playful question: what if this intricate mathematical mechanism were personified? Would ECDSA don a cape, standing valiantly against the evils of cybercrime?
At its core, ECDSA employs the mathematical principles of elliptic curves, a concept that might seem esoteric at first glance. Yet through its implementation, it offers a robust method for securing digital signatures. To comprehend ECDSA, one first needs to grasp the essential components that constitute the framework: private keys, public keys, and signatures. These entities interact in a manner that is both sophisticated and systematic.
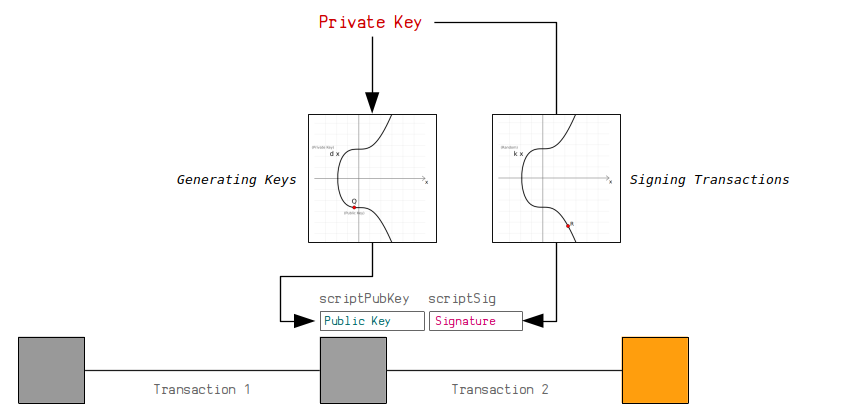
The process initiates with the selection of an elliptic curve. An elliptic curve is defined by an equation of the form y² = x³ + ax + b, where a and b are constants that ensure the curve possesses certain desirable properties. In the Bitcoin ecosystem, for instance, the chosen curve is the secp256k1. This specific curve was strategically selected for its balance between performance and security.
Once the curve has been selected, the subsequent step involves generating a private key. The private key is essentially a randomly chosen number within a predetermined range, which plays a pivotal role in both creating the public key and signing transactions. The brilliance of ECDSA lies in its ability to take this private key and apply it to the elliptic curve to yield a public key.
This transition is not a mere numerical transformation. Instead, it’s an operation embedded in the computational depths of elliptic curve mathematics, whereby scalar multiplication takes the private key and maps it to a unique point on the elliptic curve. This generated public key retains a one-to-one relationship with the private key, making it infeasible for an adversary to deduce the private key merely from the public key. This property is what imbues the system with its strength and security.
So, how is a digital signature crafted using these keys? The process begins with the data that requires verification—this could be a transaction or any data that necessitates authenticity. A cryptographic hash function, such as SHA-256, is applied to produce a fixed-length representation of the data, creating a digest. This digest is crucial because it condenses the data into a manageable, digestible form that will be used in the signing operation.
The next step involves using the private key to sign this digest. During signing, a random number, known as k, is generated for each transaction. This k should be unique and unpredictable, as reusing the same k can compromise security by revealing the private key. The signature itself comprises two parts: r and s, which are derived from the elliptic curve equations using the digest and the random number.
Delving into the mathematical minutiae, the calculations yield sustainable values that epitomize the robustness of elliptic curves. Each signature is thus uniquely tied to the specific transaction, further solidifying the integrity of the data being signed. This aspect becomes critically important, especially in financial contexts where integrity and non-repudiation are vital.
Upon receiving a signed message, the recipient can utilize the associated public key to verify the signature. This verification process checks the authenticity of the message and ensures that the relevant private key was used in signing it. The elegance of ECDSA shines through in this process, allowing users to have confidence in the assertions made by the signer.
However, what if the public key does not align with expectations? Could this divergence signify malicious intent or a technical mishap? This introduces a potential challenge—while ECDSA offers a high level of security, it is not impervious to vulnerabilities. Outcomes may be influenced by poor implementation practices, and if random number generation falters, the security assumptions can be significantly weakened.
Moreover, the significance of key management cannot be overstated. Safeguarding private keys is paramount since their exposure nullifies the very protections ECDSA provides. Adopting best practices in key storage, such as utilizing hardware wallets and multi-signature arrangements, can augment security in an ever-evolving digital landscape.
In conclusion, ECDSA stands as a centerpiece of digital assurance, robustly intertwining mathematics and computer science to secure communications. Through its meticulous generation of public keys and astute signing process, it establishes a foundation upon which cryptocurrencies, financial transactions, and various online services can operate securely. As we navigate a world increasingly augmented by technology, understanding the underlying mechanisms like ECDSA encourages informed decisions, empowering individuals against the murky waters of digital deception.





Leave a Comment