The world of cryptography is replete with ingenious methodologies devised to secure communications, yet few innovations have been as transformative as the Diffie-Hellman key exchange protocol. Imagine for a moment two parties—Alice and Bob—seeking to establish a secure line of communication over an open channel, fraught with potential eavesdroppers. How can they do so without exposing their secret to prying eyes? This intriguing scenario introduces the cornerstone of secure digital interaction: the Diffie-Hellman protocol.
First introduced by Whitfield Diffie and Martin Hellman in 1976, this key exchange method revolutionized the landscape of cryptographic strategy. Before this paradigm-shifting approach emerged, the conception of secure communication rested heavily on methods that shared keys in a physically secure manner. Such practices were often impractical in a burgeoning digital world. The Diffie-Hellman protocol presented an elegant solution: a means for two parties to create a shared secret key, all while communicating over an insecure medium.
At its core, the Diffie-Hellman protocol employs the principles of modular arithmetic and the properties of prime numbers. But how effectively does this mechanism operate? At the heart of the exchange lies a deceptively simple mathematical challenge that renders it an engaging subject for those intrigued by cryptography. Here’s how it works:
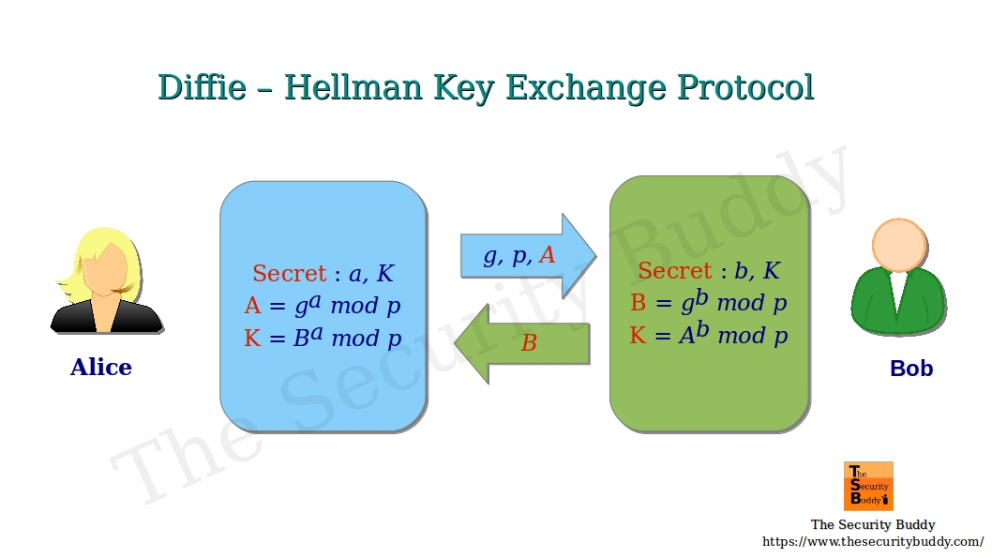
Both Alice and Bob select a large prime number ( p ) and a base ( g ), known as a primitive root modulo ( p ). The choice of these two elements is pivotal since the security of the exchanged key fundamentally relies on their arithmetic properties. Subsequently, Alice generates a private key ( a ), while Bob creates his own private key ( b ). These private keys remain confidential and are never shared.
Next, Alice raises ( g ) to the power of her private key ( a ) and takes the result modulo ( p ), creating a value known as ( A ). Bob does the same with his private key ( b ), generating a value ( B ). They then exchange these public values ( A ) and ( B ) openly across the insecure channel.
Upon receiving the other’s value, Alice computes the shared secret ( s ) by raising Bob’s public value ( B ) to the power of her private key ( a ) modulo ( p ). Conversely, Bob performs the same operation using Alice’s public value ( A ). Astonishingly, both calculations yield the same shared secret key ( s ), despite being executed independently and without prior exchange of private keys.
This lead into what can be termed a clever challenge posed by the Diffie-Hellman protocol: while the mathematics assures privacy of the shared key, how does one defend against the potential risk of a man-in-the-middle attack? Although the Diffie-Hellman method efficiently facilitates the secure exchange of keys, it is not inherently equipped to authenticate the communicating parties. In practice, this means that an adversary could intercept the public values ( A ) and ( B ), masquerading as either participant, and thus establish their own shared key with each party separately. To counteract this vulnerability, additional measures must be implemented—such as digital signatures or public key infrastructure—to authenticate users and fortify the session integrity.
Establishing a secure connection through protocols like Diffie-Hellman indeed informed the creation of other cryptographic innovations. As the demand for online privacy surged in the late 20th century, various adaptations emerged, one of which is the Elliptic Curve Diffie-Hellman (ECDH). This variant enhances security while enabling shorter keys through the use of elliptic curve cryptography, underscoring the sophistication that can evolve from the foundational principles set forth by its predecessor.
Understanding the Diffie-Hellman protocol necessitates appreciation of the delicate interplay between theoretical mathematics and practical implementation. The underlying assumptions—such as the infeasibility of calculating discrete logarithms—contribute significantly to the protocol’s robustness. In simplified terms, while one can easily compute ( g^a ) mod ( p ), deducing the value of ( a ) from ( g^a ) mod ( p ) is computationally arduous, especially for sufficiently large primes.
What is perhaps most fascinating about Diffie-Hellman is its application in modern security protocols, such as SSL and TLS, which safeguard today’s internet communications—banking transactions, private messaging, and data transfers among millions of users who rely on unyielding confidentiality. This protocol’s influence is pervasive, ingraining itself into the very fabric of our digital interactions.
To summarize, the Diffie-Hellman key exchange protocol not only marks a pivotal advancement in cryptographic communications but also elucidates a profound paradigm shift regarding the management of private information in an increasingly interconnected world. Its mathematical elegance and practical efficacy encapsulate the ingenuity required to tackle the enduring challenge of ensuring secure communications against the backdrop of cyber threats. The simplicity of its design belies its complexity, rendering it both a fundamental aspect of modern cryptography and a perennial subject of study for cryptographers and security professionals alike.
While the Diffie-Hellman protocol presents robust mechanisms for key exchange, one must remember the necessity of complementing it with robust authentication measures to truly secure the communication channel. As cryptographic needs evolve, so too must the strategies employed to fortify communications, ensuring that our digital expressions remain private, even amidst the chaos of an ever-watchful landscape.







Leave a Comment