Mathematics, often perceived as a rigid and abstract discipline, possesses a strangely poetic essence. It weaves concepts together like threads in a tapestry, forming intricate patterns that reveal profound truths. One such tapestry is that of elliptic curves. As a paragon of mathematical beauty, elliptic curves hold significant sway in various fields, from cryptography to number theory. Yet, within this domain, a question arises: What are the roots of an elliptic curve? To elicit deeper understanding, we shall delve into the structure and properties of elliptic curves, laying bare their roots both literally and metaphorically.
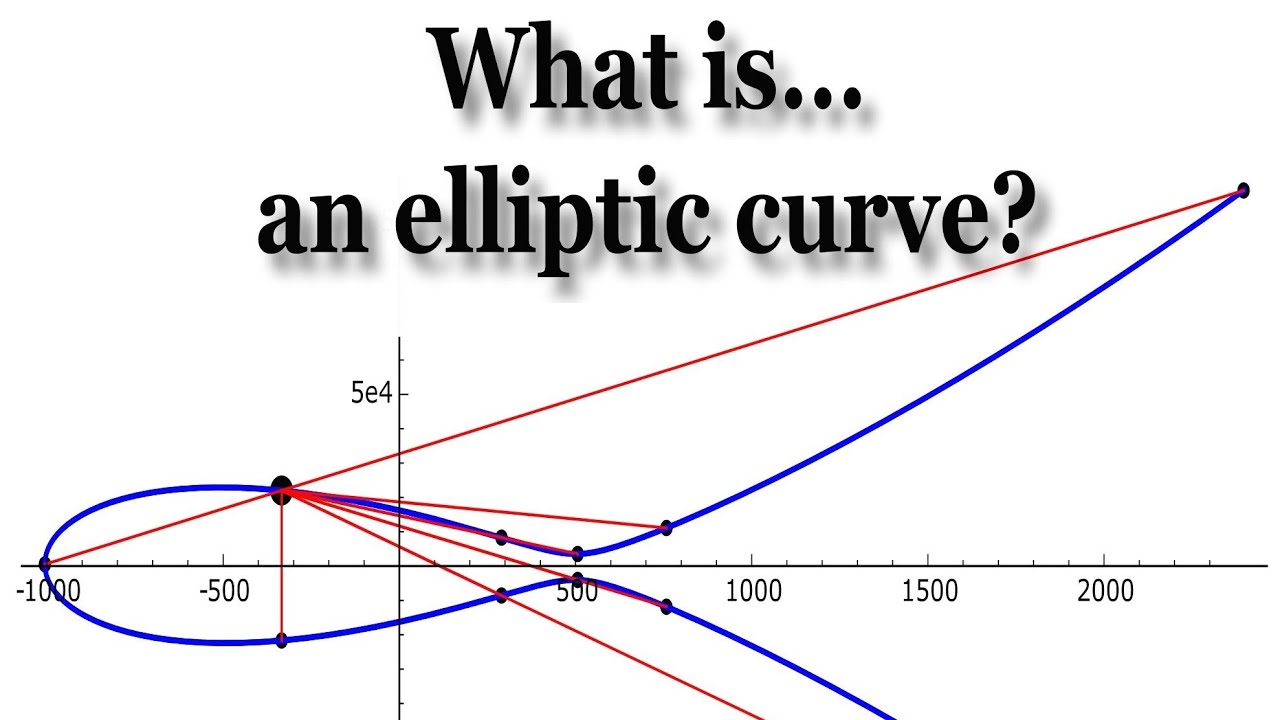
At its core, an elliptic curve is a non-singular cubic equation in two variables, typically expressed in the standard form: y² = x³ + ax + b. Here, the parameters a and b serve as the architects of the curve’s form, dictating its unique characteristics. This equation crafts a complex geometric figure, one that can be visualized as a smooth, looping shape, resembling a toroidal structure when projected onto the complex plane. The allure of elliptic curves lies not solely in their visual appeal, but in the rich mathematics they encapsulate.
To understand the roots of an elliptic curve, we must first appreciate the concept of intersection points. In algebraic geometry, the roots represent the x-coordinates where the curve intersects the x-axis and where y = 0. In practical terms, finding the roots elucidates where the curve vanishes, opening a Pandora’s box of analytical possibilities. For the elliptic curve defined above, we set y = 0, leading us to solve the cubic equation x³ + ax + b = 0—the key that unlocks our understanding of the curve’s roots.
So, how do we uncover these roots, concealed like treasures beneath the surface of the mathematical ocean? The fundamental theorem of algebra asserts that a polynomial of degree n possesses exactly n roots in the complex number system, aligning beautifully with our quest. This theorem translates to our elliptic curve, which, being cubic, must possess three roots (counting multiplicities). However, the complexities of real-world applicability often refine the search further into the realm of rational solutions.
Every cubic equation clusters its roots about its discriminant—a curious entity that signals the nature of the roots. A positive discriminant suggests three distinct roots, while a zero discriminant indicates at least two coincident roots. Conversely, a negative discriminant reveals a more elusive existence: one real root and a pair of conjugate complex roots—a hidden narrative that invites deeper exploration.
The investigation into the roots of elliptic curves also brings us to the intriguing area of field extensions. A rational root might not always reside within the confines of rational numbers alone. Sometimes, to grasp the full picture, one must traverse beyond our comfort zone of rationality into the realms of algebraic number theory. Here, the numbers evolve into more complex forms, such as irrational or even transcendental numbers, each adding layers of intrigue to our understanding.
Now, turning our attention to the conceptual significance of these roots, one may liken them to the historical figures of mythology—deities and heroes that inhabit the stories of human experience. Each root, through the unique solutions they provide, represents a facet of understanding within the elliptic curve framework. Much like Odysseus navigating through treacherous waters, mathematicians traverse the complex terrain of elliptic curves to uncover truths that contribute broadly to fields like cryptography, where security protocols rely heavily on the properties of these curves.
The unique appeal of elliptic curves also manifests in their symmetry and group structure. When distinct roots are unearthed, they behave metaphorically like members of a fellowship, forming a group under a defined addition operation. This associative property creates a mathematical symphony, enabling transformations and manipulations that enhance versatility. The intersection of these roots resonates with abstract thinking, leading to advanced applications such as the resolution of rational points, an exploration nearest to the heart of algebraic geometry.
Moreover, the roots’ unique properties serve as a linchpin in the study of the L-series and modular forms. These powerful connections have tied elliptic curves indelibly to profound conjectures in number theory, culminating in an array of results that have captivated mathematicians for centuries. The infamous Birch and Swinnerton-Dyer conjecture stands as testimony, proposing a deep link between the number of rational points on an elliptic curve and the behavior of its associated L-series at specific points.
In conclusion, the roots of an elliptic curve lie at the intersection of geometry, algebra, and number theory, weaving an intricate narrative that continues to evolve. Each root contributes to an overarching understanding of the structure and behavior of elliptic curves, forging connections that spill over into practical applications across diverse fields. As we navigate the curve’s cyclic form, one cannot escape the enchanting beauty that mathematics offers, reminding us that even in the realm of numbers and equations, a deeper, poetic resonance exists, waiting to be discovered beneath the surface.







Leave a Comment