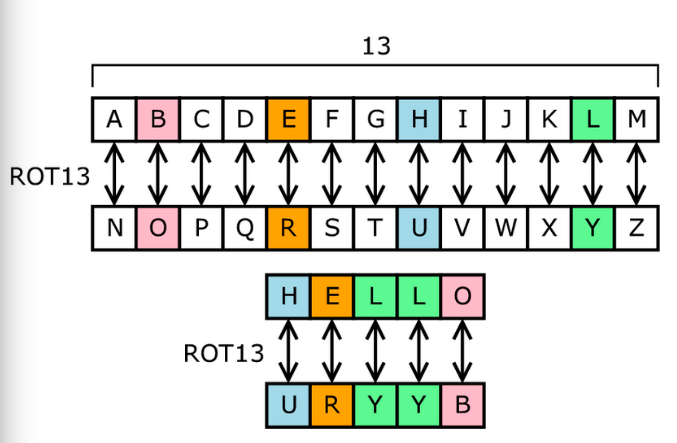
Discrete mathematics serves as the foundational bedrock for various domains in modern cryptography. A multifaceted discipline, it encompasses a range of topics including combinatorics, graph theory, number theory, and logic. Each of these sub-disciplines fosters intricate applications that bolster the security of information in our increasingly digital world. In this comprehensive exploration, we will delve into several prominent applications of discrete math in cryptography, each significantly contributing to the safeguarding of sensitive data.
1. Number Theory and Public Key Cryptography
Number theory, a vital branch of discrete mathematics, plays an instrumental role in public key cryptography. The RSA algorithm, perhaps the most recognizable example, relies heavily on the properties of prime numbers. By selecting two distinct large prime numbers and multiplying them, a public key is generated that is computationally infeasible to factor. The security of RSA hinges on the difficulty of this factorization process. An attacker would require extraordinary computational resources and time to deduce the private key from the public one, making number theory indispensable in preserving confidentiality.
Another prominent application of number theory in cryptography is the Diffie-Hellman key exchange protocol. This method allows two parties to securely share a secret key over an insecure channel. Using modular arithmetic, the algorithm’s security stems from the discrete logarithm problem, which remains efficiently solvable in one direction but defies easy resolution in reverse. The underpinning of number theory thus facilitates not only the establishment of secure communication channels but also contributes to key distribution mechanisms.
2. Combinatorics and Cryptographic Algorithms
Combinatorial mathematics directly influences the structure and security of cryptographic algorithms. The design of cryptographic systems often necessitates intricate arrangements and combinations of components to enhance security. Symmetric key algorithms, such as the Advanced Encryption Standard (AES), utilize combinatorial principles to develop complex key schedules and substitution-permutation networks. Through these methods, the algorithm guarantees that even minor alterations in the plaintext or key yield entirely different ciphertexts. The unpredictable behavior derived from combinatorial processes enhances the robustness of the encryption.
Moreover, combinatorial techniques are critical in the analysis of cryptographic protocols, helping practitioners ascertain feasible vulnerabilities and weaknesses. The application of combinatorial structures provides insights into the cipher’s resilience against various forms of attack, including brute force and cryptanalysis.
3. Graph Theory in Network Security
Graph theory emerges as a pivotal tool in the realm of network security. Generally focused on the study of graphs, which are mathematical representations of connections or relationships, this discipline enables the modelization of networks where nodes represent entities and edges signify connections. Cryptographic protocols often employ graph algorithms to ensure secure communications among various parties within a network.
For instance, the concept of spanning trees, derived from graph theory, aids in constructing secure communication networks by minimizing the potential for interception and ensuring redundancy. Furthermore, graph-based routing protocols can prevent attacks by detecting anomalies in network traffic patterns, demonstrating how discrete mathematics furnishes a layer of protection within cybersecurity frameworks.
4. Logic and Formal Verification
Logic, an essential component of discrete math, plays a crucial role in the formal verification of cryptographic algorithms and protocols. This branch addresses the principles of reasoning, enabling cryptographers to construct formal proofs that demonstrate the correctness and security of the systems in question. The validity of cryptographic implementations is paramount, and logic aids in establishing frameworks that guarantee operational integrity.
For instance, propositional logic and predicate logic can be employed to formulate security properties that must be satisfied, such as confidentiality, integrity, and authenticity. These logical structures facilitate the development of verification tools that can systematically analyze and confirm the proper functioning of cryptographic protocols, minimizing vulnerabilities and ensuring their resilience against potential adversaries.
5. Coding Theory and Error Detection
In the context of information transmission, coding theory, an extension of discrete mathematics, plays an essential role in error detection and correction. Cryptographic systems must not only secure data but also ensure its integrity during transmission. By utilizing various coding techniques, such as block codes and convolutional codes, cryptographers can facilitate reliable communication even in the presence of noise and interference.
These error-correcting codes allow a receiver to detect and correct errors that may occur during data transfer, rendering the system more resilient against data corruption. Therefore, coding theory presents an intersection between data integrity and security, further exemplifying the relevance of discrete mathematics in contemporary cryptography.
6. Complexity Theory and Security Assumptions
Finally, complexity theory, which studies computational problems and their inherent difficulty, is paramount in establishing security assumptions within cryptographic practices. Many cryptographic algorithms rely on problems deemed “hard” to solve, such as factoring large integers or computing discrete logarithms. Complexity classes, such as NP-hard problems, serve as benchmarks for evaluating the security of cryptographic protocols.
Understanding these complexities empowers cryptographers to design robust algorithms that withstand adversarial attacks. The interplay between complexity theory and cryptography ultimately informs security standards and fosters a deeper comprehension of what constitutes a feasible attack, guiding the development of future cryptographic methodologies.
In conclusion, discrete mathematics permeates numerous facets of cryptography, rendering it an indispensable tool in protecting sensitive information. From the robustness of public key frameworks grounded in number theory to the meticulous structure established through combinatorial algorithms, the contributions are manifold. Grasping the intricacies of these applications enriches our understanding of cryptographic security, ensuring that sensitive data remains protected from prying eyes in our increasingly interconnected world.






Leave a Comment