At the heart of modern cryptography lies RSA encryption, an extraordinary and widely utilized algorithm that secures digital communication through the principles of number theory. RSA, named after its inventors Rivest, Shamir, and Adleman, employs the mathematical interplay of prime numbers to facilitate secure data transmission. This article aims to demystify the intricate workings of RSA encryption, providing readers with a comprehensive step-by-step breakdown of the mathematics involved.
The foundation of RSA encryption is predicated on a few fundamental concepts in number theory: prime numbers, modular arithmetic, and the concept of public and private keys. To begin with, prime numbers are integers greater than one that have no positive divisors other than one and themselves. Common examples are 2, 3, 5, 7, 11, and so forth. The innovative aspect of RSA encryption lies in its reliance on the difficulty of factoring large composite numbers, which is a problem that becomes exponentially more challenging as the size of the numbers increases.
The initial phase of generating RSA keys involves selecting two distinct prime numbers, ( p ) and ( q ). For practical applications, these primes should be sufficiently large—in the realm of hundreds or thousands of digits. The security of the RSA algorithm is significantly bolstered by the selection of large primes, making factorization computationally intensive.
Next, we compute the modulus ( n ) used for both the public and private keys. This is derived by multiplying ( p ) and ( q ):
n = p * qHere, ( n ) serves as the modulus for the encryption and decryption processes. The product ( n ) is pivotal because it forms part of the public encryption key that pairs with an appropriate exponent.
Now, we must calculate the totient of ( n ), denoted as ( phi(n) ), which is essential for determining the public and private key pairs. The totient is given by the formula:
φ(n) = (p - 1) * (q - 1)This calculation helps to establish the number of integers less than ( n ) that are coprime to ( n ). The significance of ( φ(n) ) lies in its relation to the choice of the public exponent ( e ).
The public exponent ( e ) is chosen next. This value should fulfill two critical criteria: it must be greater than 1 and less than ( φ(n) ); moreover, ( e ) and ( φ(n) ) must be coprime (i.e., they share no common factors other than 1). A commonly used value for ( e ) is 65537, chiefly due to its propensity for efficient computation while maintaining security.
With ( e ) chosen, the next step is to compute the private exponent ( d ), which is instrumental in decryption. The value ( d ) must satisfy the following congruence relation:
d * e ≡ 1 (mod φ(n))To ascertain ( d ), one typically employs the Extended Euclidean Algorithm, which facilitates the calculation of modular inverses. Once ( d ) is computed, the trio ( (n, e) ) represents the public key, while ( (n, d) ) constitutes the private key.
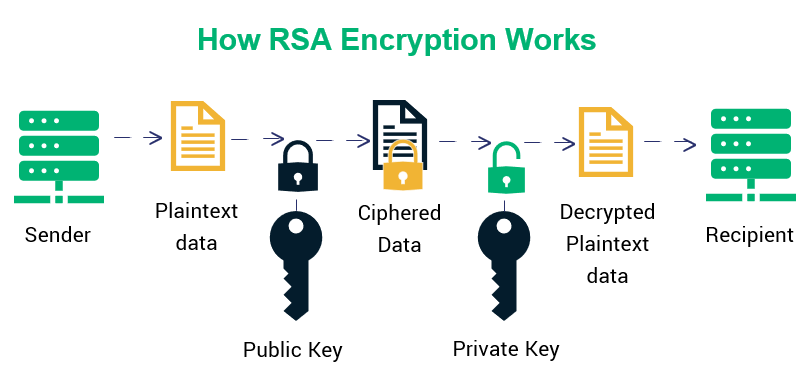
Having established the public and private keys, one can now understand the encryption and decryption processes that utilize these keys. To encrypt a plaintext message represented as an integer ( m ) (where ( 0 < m < n )), the following equation is employed:
c = m^e mod nThe resultant ( c ) is the ciphertext that can be transmitted securely. The beauty of RSA encryption lies in its asymmetric nature: only the corresponding private key ( d ) can facilitate decryption.
For decryption, the receiver utilizes their private key ( (n, d) ) to recover the original plaintext by applying the following transformation:
m = c^d mod nThus, once ( c ) is decrypted, it retrieves the initial plaintext message ( m ). This entire process, driven by the mathematical foundation of primes and modular arithmetic, underscores the robustness of RSA encryption against potential attacks.
Despite its strengths, RSA encryption is not without vulnerabilities. One notable concern is the advent of quantum computing. Quantum algorithms, such as Shor’s algorithm, threaten to erode the security RSA provides by efficiently factoring the product of large primes. Hence, contemporary research into post-quantum cryptographic systems is paramount to safeguarding against future threats.
Moreover, the utilization of small primes or poorly chosen keys can dramatically weaken RSA’s security. Therefore, it is imperative to generate keys using secure random number generators and to ensure primes are of sufficient length, typically no less than 2048 bits.
In conclusion, RSA encryption serves as a quintessential example of how mathematical principles can fortify digital communications. By comprehensively understanding the interplay of prime numbers, modular arithmetic, and public-private key generation, one can appreciate the elegance and complexity inherent in RSA. As we advance into an era of increasingly intricate computational capabilities, the need for innovative cryptographic solutions remains ever pressing.







Leave a Comment