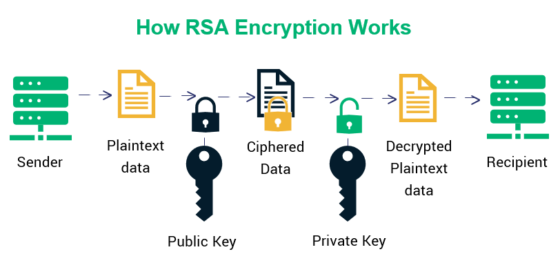
RSA, an acronym derived from the surnames of its inventors—Rivest, Shamir, and Adleman—has become the cornerstone of secure data transmission. Traditionally, the RSA algorithm relies on the mathematical properties of large prime numbers. The quintessential approach insists on the use of two distinct primes to generate the public and private keys essential for encryption and decryption. However, the intriguing notion of implementing RSA without two primes not only invites scrutiny but also evokes a broader conversation regarding the foundational principles of cryptographic protocols.
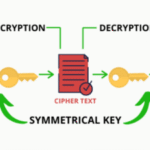
At its core, RSA operates on the basic premise of modular arithmetic, particularly the difficulty of factoring the product of two large primes, denoted as n = p * q. The security of this mechanism hinges on the idea that while it is straightforward to multiply two primes together, deriving the original primes from their product is exponentially hard. But what if we were to consider RSA-like mechanisms that sidestep this twin-prime paradigm? The exploration of this concept addresses not only theoretical implications but also practical applications and the inherent vulnerabilities that may arise.
One of the driving forces behind the fascination with RSA without two primes lies in the persistent quest for efficiency. In cryptographic systems, performance is often as crucial as security. Algorithms utilizing two prime factors face significant computational overhead, especially when dealing with large integers beyond ordinary processing capabilities. By contemplating an alternative wherein a single prime or non-prime composite suffices, the theoretical path broadens to include new avenues of exploration, favoring speed without considerable loss in security.
To better understand this, consider the scenario where RSA is adapted to utilize a single prime, p. In this case, the public key would be derived from the value of n = p^2, where the modulus becomes the product of p with itself. While superficially similar to traditional RSA, this approach inherently alters the security landscape. The process of factorization becomes trivial for any entity aware that p^2 is utilized, as mathematical ingenuity allows for straightforward extraction of p. Subsequently, the cryptographic strength diminishes significantly. The major premise of RSA—its reliance on the complexity of factorization—has been undermined, presenting a veritable chasm for potential exploitation.
A salient observation in the cryptographic community is the implicit assumption that security is synonymous with complexity. The transition away from prime multiplicands invites a dissection of this notion. Surpassing the orthodox two-prime usage may lead to considerable security deterioration unless alternative robust mechanisms are put in place. It poses an essential question: Are there truly robust methods of encryption that do not rely on the prime factorization problem, or is this a fundamental limitation of our current understanding?
Exploring RSA without two primes necessitates an engagement with fundamental concepts in number theory. Alternative composites or algebraic structures, like rings, may provide fertile ground for developing new cryptographic schemes. For instance, elliptic curve cryptography (ECC) operates on the principles of elliptic curves rather than prime factorization, thus facilitating enhanced security with significantly smaller keys. However, this leads to an ironic contemplation; embracing non-standard constructs amplifies complex mathematical understanding while shunning the very simplicity that organizations seek for usability.
Despite these considerations, it is pivotal to challenge the misconceptions surrounding the exclusion of two primes. Innovation in cryptography does not merely revolve around reconfiguring traditional methods; it beckons for revolutionary thinking. For instance, hybrid systems that amalgamate various cryptographic approaches could yield a more resilient framework. This intersection might resolve the concerns of performance while maintaining a requisite level of security. It conjures a layer of abstract reasoning that transcends the binary consideration of primes versus composites, pushing towards a more holistic grasp of encryption paradigms.
Furthermore, the implications of utilizing only a single prime or composite extend beyond theoretical musings. Such explorations bear potential for practical application within specific domains. In constrained environments, like Internet of Things (IoT) devices, resource limitations necessitate a departure from computationally intensive operations. Here, a simplistic encryption method might find its niche, provided that ambient risks are meticulously managed. However, integrating this model into mainstream systems requires profound deliberation, as the balance of immediacy against long-term sustainability looms large.
On the horizon of cryptographic evolution, the prospect of operating outside the traditional two-prime RSA warrants a rigorous investigation of parallel security channels. Are there explicit methodologies that strengthen encryption independent of conventional prime dependencies? This captivating query teeters between speculative theory and radical implementation. Each response invites further inquiry into the underlying mathematical constructs shaping our digital security landscape.
In essence, while the conjecture of executing RSA without two primes may surface as a niche novelty, it provokes an invaluable dialogue around the rules that govern our encryption methodologies. Emphasizing innovation, the cryptographic field remains ripe for exploration. The potential to innovate within its seams holds both peril and promise. Within this intricate interplay, the quest for efficiency, security, and simplicity will continue to compel attention, rewriting the narratives of established norms in providing secure communications.







Leave a Comment