In the realm of cryptography, the choice of algorithm can lead to varying degrees of security and computational efficiency. With a plethora of algorithms available, RSA (Rivest-Shamir-Adleman) and ECDSA (Elliptic Curve Digital Signature Algorithm) are two of the most prominent contenders in public key cryptography. This discourse will dissect these two algorithms, highlighting their mechanisms, advantages, considerations, and overall landscape in which they operate.
Understanding RSA:
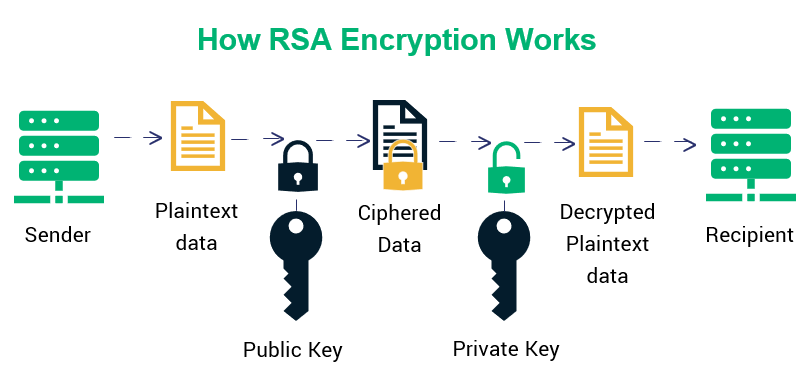
At its inception, RSA revolutionized the field of cryptography by providing a method for secure key exchange. RSA relies on the mathematical complexity of factoring large integers, specifically the product of two prime numbers. The security of RSA scales with the size of these primes; larger keys lead to increased security but at the cost of performance. Typically, RSA keys range from 2048 to 4096 bits, allowing for robust encryption capabilities.
In its operation, RSA employs a pair of keys: a public key for encryption and a private key for decryption. This asymmetry allows individuals to share their public key openly while safeguarding their private key. The encryption process involves raising the plaintext message to an exponent defined by the public key, followed by a modulo operation with a product of the primes. Decryption reverses this process.
Understanding ECDSA:
In contrast to RSA, ECDSA is built on the principles of elliptic curve cryptography. It utilizes the algebraic structure of elliptic curves over finite fields, which allows for the creation of keys that are much shorter than those used in RSA, yet equally secure. For instance, a 256-bit key in ECDSA offers comparable security to a 3072-bit RSA key. This efficiency is particularly advantageous in resource-constrained environments, such as mobile devices and Internet of Things (IoT) applications.
The operational mechanics of ECDSA differ significantly from RSA. In ECDSA, a private key generates a public key point on the elliptic curve. The signing process involves a randomized number and uses elliptic curve multiplications, while the verification process involves checking the signature against the public key. This intricate dance of mathematics provides robust guarantees of authenticity and integrity in digital communications.
Performance and Scalability:
When discussing performance, ECDSA demonstrates a significant edge over RSA. Given that ECDSA keys are shorter while delivering equivalent security levels, they require less computational power for both signing and verification processes. This trait not only makes ECDSA faster but also reduces bandwidth consumption—an issue that frequently arises in data transmission over networks. In terms of scalability, ECDSA is better suited to applications needing high throughput and secure channels.
Security Considerations:
While both RSA and ECDSA are robust cryptographic methods, their security is contingent on different underlying mathematical problems. RSA’s security hinges on the difficulty of integer factorization, which, despite advancements in algorithms and computational power, remains a formidable challenge for large primes. Conversely, ECDSA’s strength relies on the elliptic curve discrete logarithm problem, which is currently regarded as more difficult to solve than integer factorization. Thus, in theoretical terms, even though both algorithms are strong, ECDSA often presents a higher security margin for smaller key sizes.
Additionally, post-quantum cryptography poses a future threat to both algorithms. Quantum computers, under development, may efficiently solve the problems that underpin these cryptographic methods, thereby rendering them vulnerable. Research is ongoing to develop quantum-resistant algorithms that can withstand such advancements.
Implementation and Adoption:
Adoption of RSA has pervaded various sectors due to its long-standing history and widespread recognition. It integrates seamlessly into established protocols such as SSL/TLS for secure web communications. However, its relative inefficiency compared to ECDSA has prompted a gradual shift toward elliptic curve solutions, particularly in modern applications.
On the other hand, ECDSA has garnered significant traction in modern frameworks, especially in blockchain technologies and secure communications in mobile applications. Its championing by institutions like the National Institute of Standards and Technology (NIST) as a standard for digital signatures further solidifies its position in the evolving cryptographic landscape.
The Future Landscape:
As technology progresses, the cryptographic community must remain vigilant. The rise of quantum computing necessitates a proactive approach towards adopting algorithms that can withstand quantum threats. Hybrid cryptographic systems, which combine the strengths of multiple algorithms, and the development of new paradigms like lattice-based cryptography may provide solutions.
In the battle of RSA vs. ECDSA, while RSA continues to be a stalwart due to its entrenched position within legacy systems, ECDSA’s efficiency and security scalability position it as a formidable competitor for modern applications. Ultimately, the choice of algorithm hinges upon the specific requirements of each use case—balancing security, performance, and future-proofing against impending technological advancements.
As cryptography evolves, so too must the technologies and frameworks that rely upon it. The discourse surrounding RSA and ECDSA underscores the importance of understanding not only the mathematical foundations of these algorithms but also their implications on the broader landscape of digital security.







Leave a Comment