In the realm of computer science and cybersecurity, few cryptographic algorithms capture the imagination as emphatically as RSA. Renowned for its elegance and effectiveness, RSA stands as a formidable guardian of digital communications. At its heart lies a fascinating interplay between number theory and practical application, drawing attention from mathematicians, computer scientists, and security professionals alike.
The genesis of RSA, which stands for Rivest, Shamir, and Adleman—its creators—is an epochal moment in cryptographic history. Intriguingly, the allure of RSA does not solely stem from its capacity to protect sensitive information; it is also deeply rooted in the underlying mathematics that govern its operation. To appreciate RSA’s significance, one must delve into the branches of prime factorization, modular arithmetic, and the enigmatic principles of discrete logarithms.
One cannot discuss RSA without acknowledging the pivotal role of large prime numbers. The strength of RSA encryption relies fundamentally on the mathematical difficulty of factorizing a product of two large primes. This product forms the basis for the public key, which is disseminated broadly, while the private key—derived from the prime factors—remains secret. The essence of RSA’s security is thus underscored by the theorem that posits while multiplying two primes is computationally trivial, reversing the process—factorization—is non-trivial, especially as the number size escalates.
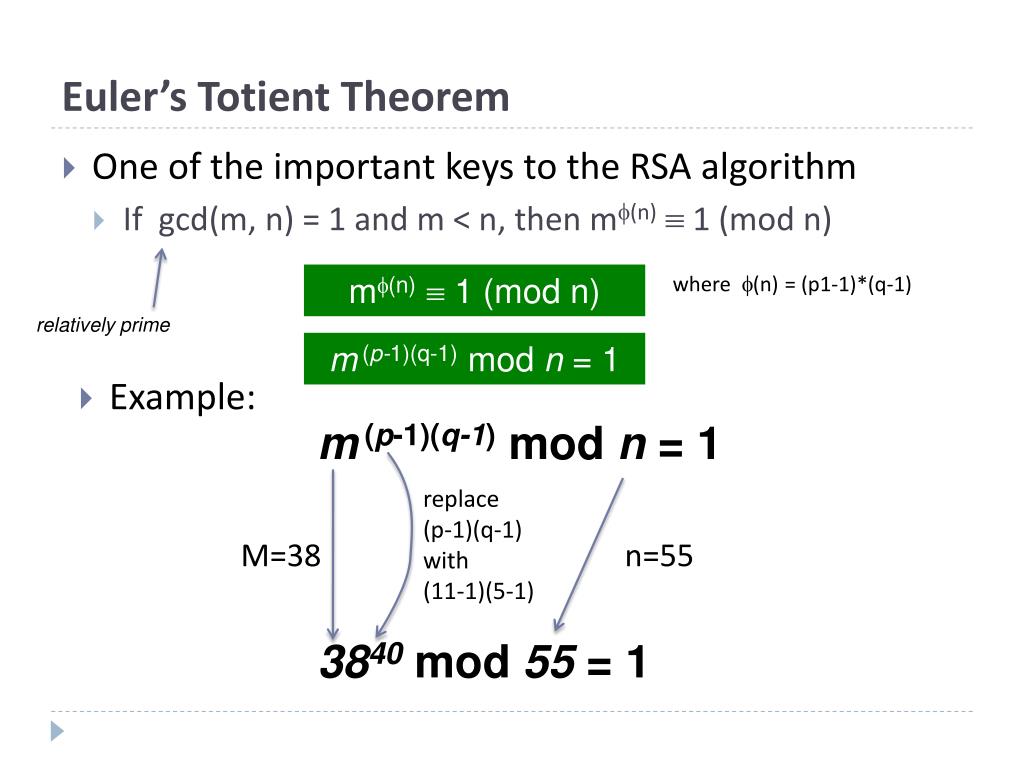
A common observation among enthusiasts is the sheer magic of RSA’s key generation process. It begins with the selection of two distinct large prime numbers, typically denoted as p and q. The product of these primes, n = p*q, constitutes the modulus for both the public and private keys. The following step involves calculating the totient function, φ(n) = (p-1)(q-1), which plays a crucial role in determining the keys that allow encryption and decryption. It is here that Euler’s Totient Theorem comes into play, forming the theoretical backbone of RSA’s security. The theorem provides the foundation for the key creation process, transforming what could seem like arbitrary numbers into a structured method of encryption.
Transitioning from theory to practice, the processes of key generation, encryption, and decryption in RSA provide fertile ground for examination. The public key comprises the modulus n and an exponent e, which is chosen such that it is coprime to φ(n). The private key, conversely, is derived from e’s multiplicative inverse modulo φ(n). The elegance of the RSA algorithm lies in its simplicity; one can encrypt a plaintext message m using the public key with the formula: c = m^e mod n. This transforms the plaintext into ciphertext, which can only be decrypted by the bearer of the private key using the formula: m = c^d mod n, where d is the private key exponent.
But what encapsulates the fascination surrounding RSA goes beyond mathematics; it encompasses its practical implications. RSA serves as the underpinning of numerous secure communication protocols, such as HTTPS, ensuring that the data transmitted over the internet remains confidential. By safeguarding financial transactions and personal communications, RSA has become a foundational element of modern digital life. Its deployment is not limited to websites; it extends to securing emails, virtual private networks (VPNs), and other forms of digital correspondence, creating a robust layer of cybersecurity.
Yet, as one delves deeper into the RSA framework, the complexities and vulnerabilities begin to unravel. The algorithm, while robust against certain forms of attack, is not impervious. Advances in computational power, particularly with the advent of quantum computing, herald potential threats to RSA’s efficacy. Shor’s algorithm, for instance, poses a significant risk by providing the means to factor large numbers efficiently, thereby undermining the very foundation of RSA encryption.
This looming threat elicits a broader contemplation about the future of cryptography. The necessity for developing quantum-resistant algorithms has never been more pronounced. The mathematical intricacies that underpin RSA’s magic necessitate an ongoing vigilance and a willingness to innovate as technology evolves.
Moreover, the ethical considerations surrounding the use of RSA and similar algorithms should be acknowledged. The dual-use nature of cryptographic techniques presents a moral quandary. While tools like RSA are instrumental in protecting privacy and securing communications, they can also be exploited by malicious entities to perpetrate cybercrimes. This dichotomy brings forth the debate over encryption backdoors, where governments may seek access to encrypted information under the guise of national security. Such discussions capture the intersection of technology, ethics, and societal implications, revealing the multifaceted nature of RSA’s role in the digital age.
Ultimately, RSA is emblematic of a grander narrative within computer science—a narrative rich in mathematical beauty, practical necessity, and ethical considerations. The algorithm serves not merely as a solution to a computational problem but as a beacon of creativity harnessed to navigate the complexities of the digital frontier. As cryptographers continue to unravel the mysteries of number theory and explore the implications of quantum computing, the legacy and evolution of RSA will certainly remain a captivating subject for exploration and discussion.







Leave a Comment