In the digital age, the importance of data privacy cannot be overstated. Imagine securing your secret messages from prying eyes while ensuring they reach the intended recipient unharmed. This is where RSA encryption (Rivest–Shamir–Adleman), named after its inventors, becomes an essential tool in the realm of cryptography. Have you ever pondered how your online transactions and private communications remain secure? Let’s explore the intricate dance of locking and unlocking digital secrets through RSA encryption.
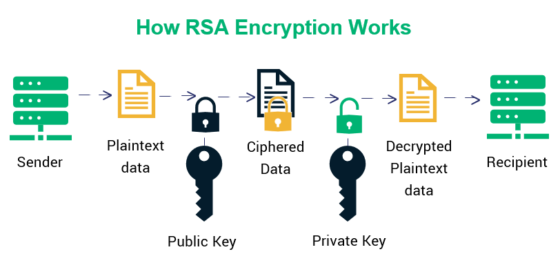
At its core, RSA is a public-key cryptographic system that enables secure data transmission. Unlike symmetric key algorithms that use a single secret key for both encryption and decryption, RSA employs two distinct keys: a public key, which anyone can access, and a private key, known only to the recipient. This distinction presents both an intriguing challenge and a delightful puzzle. How can data stay secure when one of the keys is widely available?
The foundation of RSA lies in the mathematical properties of prime numbers. It begins with the selection of two prime numbers, typically denoted as p and q. These primes are large—often hundreds of digits long—rendering their factorization computationally prohibitive. The security of RSA hinges on the difficulty of factoring the product of these primes, known as n, because while it is easy to multiply p and q to obtain n, reversing the process is computationally intense.
Next, the public key comprises the modulus n and an exponent e, usually a small prime number such as 65537, which helps facilitate the encryption process. The private key is derived from n, p, q, and another value d, which is calculated using the modulus inverse. In essence, the public key allows anyone to lock up information securely while the private key locks and unlocks the treasures.
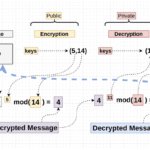
When encrypting a piece of data, let’s consider a plaintext message M. The encryption process produces a ciphertext C using the formula:
C ≡ Me (mod n)
Here, the plaintext message is raised to the power of the public exponent and then taken modulo n. The result is a seemingly jumbled cascade of numbers that bears no resemblance to the original message. Yet, only the holder of the private key can decode this ciphertext back into its original form.
So, what happens during decryption? The recipient employs their private key to convert the ciphertext back into the plaintext. The decryption formula is akin to the encryption formula but utilizes the private exponent d:
M ≡ Cd (mod n)
By applying the private key, the recipient can unveil the concealed message, deserving of its rightful place back in the realm of clarity. The elegance of this dual-key system ensures that even if someone intercepts the encrypted message, without the private key, all they hold is an enigma.
However, the allure of RSA encryption is not without its vulnerabilities. One noteworthy challenge is related to the key length. As computational power increases, shorter keys are rendered insecure against brute-force attacks. Consequently, RSA keys are generally recommended to be at least 2048 bits long to ensure robust protection against unauthorized access. The increasing prevalence of quantum computing also casts a shadow of uncertainty over RSA’s future, prompting a search for more resilient cryptographic algorithms.
The environmental context of RSA encryption is equally dire. As data breaches proliferate in our hyper-connected world, relying solely on one method of encryption becomes a precarious strategy. Yet, the beauty of RSA is not just in its security; it’s also in its versatility. Organizations universally apply it to secure communications, digital signatures, and certificate authorities, among other use cases.
Still, with great power comes great responsibility. Implementers must ensure their key management practices uphold the integrity of the encryption. This extends beyond mere storage; it includes rigorous access controls and regular key rotations to minimize the risk of exploitation. Consider multiple layers of security as vital in an ever-evolving threat landscape.
In summation, RSA encryption stands as a stalwart guardian of digital secrets, embodying both simplicity and complexity in its mathematical foundations. The interplay between public and private keys creates a robust framework that ensures confidentiality, integrity, and authenticity across countless applications. While challenges persist, they serve not as deterrents but as encourages for continued innovation within the cryptographic realm.
As we continue to navigate an increasingly digital world rife with uncertainties, understanding and employing RSA encryption tasks us with a curious pursuit: How effectively can we safeguard our secrets, and how can we adapt to evolving threats? The answers remain as dynamic as technology itself, inviting us to engage both critically and creatively in the realms of security.




Leave a Comment