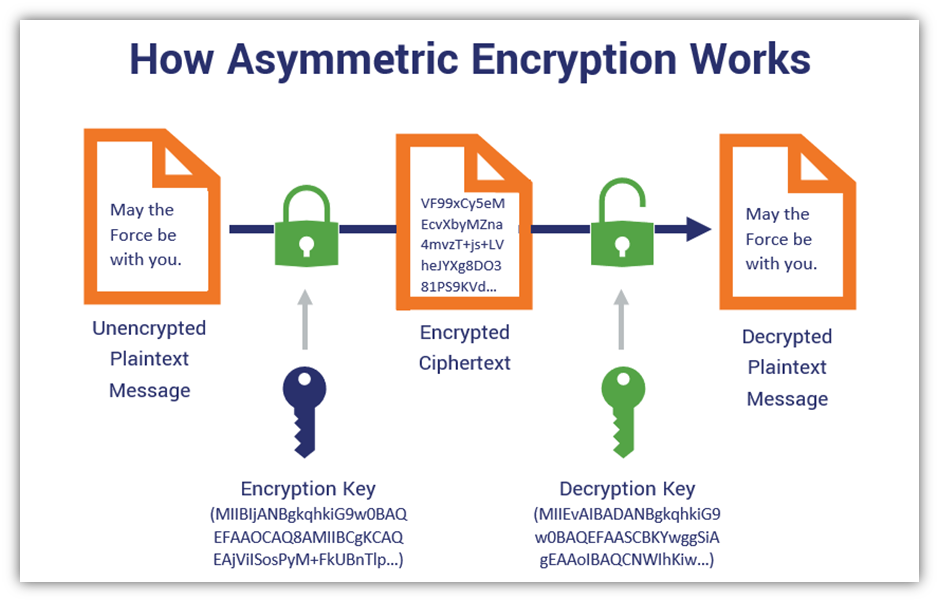
In the vast landscape of cryptography, reminiscent of a sprawling garden filled with intricate patterns, asymmetric encryption stands as a unique flower. Unlike its symmetric counterpart, where both sender and receiver share a common key akin to a secret handshake, asymmetric encryption utilizes a pair of keys—a public key that blooms openly for all to see, and a private key, coveted and concealed. The crux of asymmetric encryption lies in its mathematical foundations, inviting profound inquiry: is there such a thing as mathematically secure asymmetric encryption?
To explore this query, one must first understand the very principles that underpin asymmetric encryption. At its essence, it thrives on mathematical ideals, specifically the concept of one-way functions. These functions are analogous to a roaring river, flowing in one direction, where it is simple to traverse downstream but extraordinarily complex to swim upstream. One-way functions serve as the backbone of asymmetric cryptography; they allow the creation of a public key from a private key while making it computationally infeasible to derive the private key from the public key.
This leads us to examine the cornerstone of many asymmetric encryption schemes: the RSA algorithm. The security of RSA is predicated on the difficulty of factoring the product of two large prime numbers—an operation that remains arduous even for formidable computing systems. Imagine attempting to piece together a shattered vase; identifying and understanding the individual pieces does not automatically provide the means to reassemble them. In a similar vein, while the public key can be distributed widely, reverse engineering it to unveil the private key requires unfathomable computational resources, particularly when dealing with an adequately large key size. However, this raises an essential question: how easily can these mathematical challenges evolve?
The evolution of computational power has not gone unnoticed. Just as flora adapts to its environment, advances in technology, such as quantum computing, may render current cryptographic systems vulnerable. Quantum algorithms, such as Shor’s algorithm, present a formidable threat, heralding a future where the complexities of factoring could diminish significantly under a quantum regime. As traditional methods generate new growth, the foundational security of asymmetrical encryption becomes increasingly tenuous. Thus, one cannot claim absolute mathematical security in an ever-evolving ecosystem of cryptographic threats.
Yet, amidst this uncertainty, research continues to burgeon, much like weeds competing for sunlight in a garden. Post-quantum cryptography proposes a diverse array of new cryptographic techniques designed to withstand quantum attacks. Many of these new algorithms employ mathematical structures that are inherently resistant to the vulnerabilities exposed by quantum computing. For instance, lattice-based cryptography, which leverages geometric shapes in high-dimensional spaces, presents a promising avenue to establish more secure asymmetric systems. It is as if the garden, with its various plant species, adapts and rearranges itself to flourish, regardless of external challenges.
However, while it is vital to explore avenues for enhanced security, it is equally essential to consider the implications of security beyond mere mathematics. The notion of ‘what is secure?’ extends beyond mathematical constructs and into realms of implementation, human error, and operational security. The best-designed cryptographic system is futile if poorly managed. It is crucial to recognize that asymmetric encryption, though robust in theory, is not impervious to vulnerabilities introduced by weak key management practices or software bugs. Even the most refined techniques in the garden can experience decay if not nurtured properly.
So, is there mathematically secure asymmetric encryption? The answer hinges on several factors: the evolving nature of computational capabilities, the ingenuity of cryptographic adversaries, and the fragility of human implementation. While no form of encryption can claim unassailable security indefinitely, the continued innovation in mathematical frameworks and protective measures instills confidence. The cryptographic landscape is dynamic, akin to a perennial garden undergoing seasonal changes.
The interplay between asymmetry in encryption and the mathematical foundations that support it should not be viewed in isolation. The interdependencies between mathematical ingenuity, technological advancement, and practical implementation collectively contribute to the overall security posture of asymmetrical systems. Current challenges, such as the rise of quantum computing, may serve as a catalyst for further innovation and resilience in the field.
Ultimately, the future of asymmetric encryption will not dwell in the realm of absolute certainty. Instead, it will paint a picture of ongoing evolution, where mathematicians and cryptographers collaboratively forge new paths in response to emerging threats. As the landscape of security continues to shift, resilience, adaptability, and foresight shall increasingly be the watchwords of an increasingly complex digital age—a vibrant garden cultivated through knowledge and attention, rather than a perfect, static structure devoid of life.






Leave a Comment