The Secure Hash Algorithm 256 (SHA-256) stands as a pillar in the cryptographic community. This enigmatic algorithm, a member of the SHA-2 family, is widely utilized in various applications ranging from data integrity checks to digital signatures. However, an ever-burning question plagues many cryptographic experts: Is SHA-256 unique, or can it collide? To grasp this intricate matter, one must delve deeper into the realms of cryptography and the mathematics that underpin it.
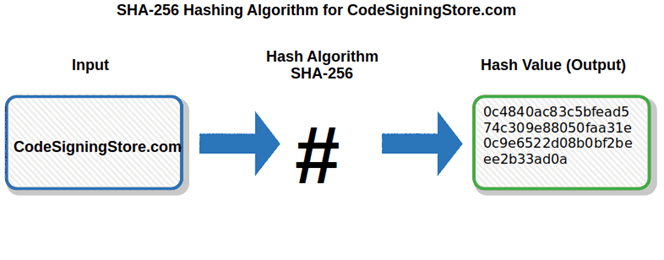
First, it is vital to comprehend the essence of a hash function. At its core, a hash function transforms input data of arbitrary length into a fixed-length string of characters, typically expressed in hexadecimal format. SHA-256 generates a hash that comprises 256 bits, yielding approximately 2256 distinct hash values. This enormous range ostensibly lends itself to a unique representation of virtually any dataset fed into the algorithm’s maw.
However, the mathematical principle underpinning hash functions is subject to the pigeonhole principle; given that the hash output is finite but the input space is infinite, it follows that collisions—where two distinct inputs yield the same hash value—are theoretically possible. This realization can cast a shadow of doubt upon the perceived uniqueness of SHA-256.
To visualize the ramifications of collisions, consider the implications of a birthday paradox. As the number of unique inputs increases, the probability of encountering two distinct entries producing the same hash value swells surreptitiously. With SHA-256, while the upper limit of potential outputs is unfathomably vast, as the number of inputs approaches this limit, the odds of collision progressively increase. Nevertheless, for practical purposes, the sheer scale of the potential output makes exploiting collisions in SHA-256 highly improbable.
Historically, earlier cryptographic hash functions such as MD5 and SHA-1 succumbed to vulnerabilities where existing collisions could be engineered. These flaws prompted a shift away from these algorithms, breeding suspicion and concern in the security landscape. SHA-1’s demise serves as a cautionary tale, compelling cryptographers and developers to endorse more robust alternatives like SHA-256. Yet the robustness of SHA-256 rests not solely on its size but the intricate functioning behind its construction.
SHA-256 employs a meticulous series of bitwise functions, message scheduling, and modular arithmetic that engages the input data in a complex ballet of manipulation. Each transformation meticulously alters the bits, rendering the output not merely an extracted fingerprint of the input, but rather a comprehensive representation of the underlying data. Its resilience against collision attacks stems from this elaborate design—an interlacing of precision and chaos that neither can be easily reverse-engineered nor imitated without exhaustive computational resources.
In light of theoretical concerns, one must evaluate the cryptographic community’s consensus regarding SHA-256’s security. As of now, no one has publicly demonstrated a practical collision, which bolsters its integrity as a go-to hash function for securing transactions and data. The algorithm’s current standing within the National Institute of Standards and Technology (NIST) further corroborates its reliability, as it remains an endorsed standard for data security protocols.
However, with every epoch in technology comes evolution. The emergence of quantum computing poses existential questions about traditional cryptographic measures, including SHA-256. Quantum algorithms like Grover’s algorithm can hypothetically accelerate the process of attempting to find collisions, thus shrinking the effective key space to half its intended size. While SHA-256 remains robust against classical attacks, the looming prevalence of quantum computing could challenge its longstanding supremacy, necessitating the exploration of next-generation hashing algorithms.
What is intriguing about the discussion surrounding SHA-256 is not only its mathematical foundation but also the philosophical implications it raises within the context of digital security. The notion of “uniqueness” is inherently tied to trust, an essential component of our digital interaction in today’s world. As digital entities increasingly rely on cryptographic assurances for confidential transactions and data integrity, the stakes rise considerably. To trust in a system that may potentially yield collisions evokes deep contemplation about security architectures in the digital age.
Moreover, embracing a broader perspective on cryptography necessitates understanding its limitations and continually assessing trust through rigorous scrutiny of existing algorithms. Despite SHA-256’s prevailing acceptance, an essential inquiry remains: how can we prepare for future upheavals in computational methods that might render even our most stalwart defenses vulnerable?
In conclusion, while SHA-256 is currently regarded as a deeply reliable hash function with an astronomically low likelihood of collision in practical scenarios, it is not entirely exempt from theoretical collision possibilities. An analytical approach to cryptography demands an oscillation between trust and skepticism, navigating the landscape of evolving technology. The question of uniqueness must be revisited periodically, inviting a sustained discussion among cryptographers, technologists, and end users alike.
Each decision to adopt a cryptographic standard carries implications not just for technological efficacy but also for the societal framework that relies on such measures for security, privacy, and trust. The saga of SHA-256 may be illustrative of our deeper quest for reliability in an increasingly uncertain digital future.







Leave a Comment