Cryptography, an ostensibly esoteric field, serves as the bedrock of digital security in our interconnected world. It endows privacy, integrity, and authenticity, transforming mundane data into something nearly impenetrable. However, the question looms large: is mathematics truly the sine qua non of cryptography? This inquiry leads us into a realm where numbers and algorithms intersect, revealing a fascinating tapestry of complexity that undergirds our digital lives.
To comprehend the significance of mathematics in cryptography, it is vital to deconstruct both concepts individually. Cryptography, at its core, is the art of encoding messages to safeguard them from prying eyes. Conversely, mathematics is the language through which these encodings are articulated. The interplay between these two disciplines is not merely superficial; it is profoundly intertwined, with the efficacy of cryptographic systems hinging on mathematical principles.
Historically, cryptography traces its lineage back to ancient civilizations. From the simple Caesar cipher, where letters were shifted through the alphabet, to contemporary algorithms that underpin secure communications on the Internet, mathematics has always played a pivotal role. The evolution of cryptography showcases an escalating reliance on mathematical sophistication: where initial techniques employed basic algebra and substitution, modern cryptography leverages advanced number theory, abstract algebra, and computational complexity.
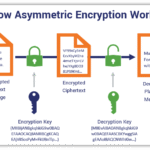
One of the principal frameworks through which cryptography operates is asymmetric encryption. This architecture, which employs two keys—a public and a private key—relies heavily on mathematical constructs, specifically prime factorization and modular arithmetic. The ostensibly unyielding difficulty of factoring large primes into their constituent elements forms the crux of the security of algorithms such as RSA (Rivest-Shamir-Adleman). Here, the mathematical principle of what is known as NP-completeness guarantees that, while multiplication of primes is straightforward, the reverse operation is computationally intense, thus providing a formidable barrier to unauthorized access.
Nonetheless, this reliance on mathematical rigor begs the question: what if the very underpinnings of these mathematical principles were to falter? The advent of quantum computing has engendered both excitement and apprehension within the cryptographic community. Quantum algorithms, such as Shor’s algorithm, threaten to dismantle the foundational security of many currently employed systems. The inevitable augmentation of computational power compels a reevaluation of prevalent cryptographic protocols. This impending paradigm shift catalyzes fresh mathematical explorations, steering researchers toward post-quantum cryptography, wherein alternative mathematical challenges are devised to guard against these futuristic threats.
As we probe deeper into the realm of mathematics in cryptography, it is prudent to acknowledge the indispensable role of mathematical proofs. Cryptographic protocols are not merely proposed without substantiation; they undergo rigorous validation via proofs that meticulously delineate their resilience against various forms of attack. These proofs integrate logical constructs, probability theory, and computational assumptions, encapsulating the intricate arithmetic that titillates a mathematician’s mind. Each established theorem spawns confidence, anchoring the reliability of our digital interactions.
Moreover, the synergy between mathematics and cryptography extends into the realm of hashing functions. Hash functions, critical for data integrity and authentication, employ complex mathematical mappings to transform arbitrary input into fixed-size outputs. The avalanche effect ensures that minute alterations yield drastically different outputs, fortifying the unpredictability required in secure communications. The impracticality of reverse-engineering these outputs underpins various applications, from safeguarding passwords to verifying digital signatures.
Yet, even amidst this mathematical majesty, one must remain cognizant of the limits of mathematics in cryptography. Practical implementation challenges arise, influencing the deployment of cryptographic systems. Real-world applications necessitate a keen understanding of not only mathematical abstractions but also system architectures and threat landscapes. A cryptographic algorithm may be mathematically impeccable, yet deficiencies in its application can expose vulnerabilities, compromising the entire system. This highlights the imperative for cryptographers to possess multifaceted expertise that transcends mere numerical prowess.
Furthermore, the mathematical foundations of cryptography encourage an ingenious paradigm shift. They compel practitioners not only to think critically about security challenges but also to engage in a continuous exploration of new mathematical territories. Each iterative advancement in cryptographic techniques propels the field forward, generating fresh insights and novel methodologies. This dynamic interplay cultivates an environment ripe for innovation, ensuring that cryptography remains adaptable to emerging threats.
In conclusion, while one could conjecture that cryptography may exist without mathematics, such an assertion belies the intricate interdependencies comprising modern cryptographic systems. Mathematics is not merely an auxiliary tool; it is the architecture that supports, enhances, and obfuscates our digital communications. As we gaze into the future, confronting both challenges and opportunities, a profound appreciation for the role of mathematics in cryptography emerges. The union of these two realms promises to redefine our understanding of security in the digital age, offering a compass as we navigate the complexities of an increasingly interconnected world.







Leave a Comment