The interplay between cryptography and its mathematical foundation offers a rich tapestry for exploration, weaving together the realms of applied mathematics and computer science. At first glance, one might perceive cryptography as a simple amalgamation of algorithmic sophistication and numerical intricacies. However, this domain embodies much more, possessing nuanced layers that invite rigorous examination. This discourse aims to dissect the intricate relationship between cryptography, applied mathematics, and computer science, providing a comprehensive understanding of this seminal field.
To begin with, applied mathematics serves as the backbone of cryptographic systems. This discipline encompasses a wide array of mathematical techniques and concepts that are indispensable in solving practical problems. Within the cryptographic landscape, concepts such as number theory, algebra, and combinatorics come to the forefront. For instance, the RSA encryption algorithm relies heavily on the properties of prime numbers—an area distinctly rooted in number theory. The key generation process, entailing the multiplication of two large prime numbers, exemplifies applied mathematical principles in action.
Turning the lens towards computer science, it becomes evident that it plays an equally pivotal role in the implementation and optimization of cryptographic techniques. Computer science provides the algorithmic frameworks necessary to deploy cryptographic solutions on digital platforms. It is within this sphere that cryptographic protocols are engineered, ensuring that information remains confidential and secure from prying eyes. The synthesis of mathematical theories with computational mechanisms yields robust encryption systems, thus establishing a symbiotic relationship between the two fields.
Yet, this relationship is not one of mere juxtaposition; rather, it resembles a delicately balanced seesaw, where progress in one domain propels advancements in the other. Consider the evolution of encryption methodologies over the decades. During the early stages of digital communications, simple substitution and transposition ciphers were prevalent, primarily grounded in classic mathematical principles. However, as computational power surged and cyber threats evolved, there emerged a pressing need for more sophisticated encryption techniques. This necessity catalyzed the development of complex algorithms, such as the Advanced Encryption Standard (AES), which marries deep-rooted mathematical theories with cutting-edge computational strategies.
In this context, it is prudent to delve into the concept of security proofs, which are fundamental to cryptography. Security proofs anchor theoretical constructs in practical implications, often deploying intricate mathematical frameworks to substantiate claims of robustness. For instance, zero-knowledge proofs allow one party to prove possession of certain information without revealing the information itself. Such constructions epitomize the marriage of abstract mathematical reasoning with practical cryptographic application—a vivid illustration of the interplay between the two fields.
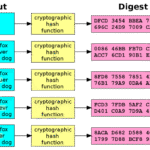
Moreover, the allure of cryptography extends beyond theoretical constructs to encompass the multifaceted world of applications. Beyond simply securing communications, cryptography finds its footing in digital currencies, secure voting systems, and even blockchain technology. Each of these applications relies on a foundation of mathematical principles tailored for computational efficiency and efficacy. The global rise of cryptocurrencies illustrates this phenomenon. The cryptography underpinning Bitcoin hinges on mathematical concepts such as hash functions and digital signatures, reinforcing the necessity of both applied mathematics and computer science in this groundbreaking technological arena.
The fabric of cryptography is further enriched by the ever-looming significance of quantum computing. As the specter of quantum capabilities threatens classical encryption methods, new mathematical paradigms must be explored to preserve information security. Quantum-resistant algorithms are areas of intense research, demanding an intricate understanding of both mathematical theories—specifically, lattice problems and error-correcting codes—and computational complexities inherent to quantum computing. This exemplifies how cryptography is a dynamic domain, in perpetual flux, where advancements in one area compel evolution in the other.
In addition, consider the philosophical implications of cryptography’s duality as mathematics and computer science. The enigmatic nature of this field invites a metaphorical interpretation akin to that of a labyrinth—each twist and turn representing a mathematical theorem, while the walls and pathways symbolize the computational frameworks that navigate through complexities. Just as a traveler in a labyrinth must balance their knowledge of its structure with the intuition of where to proceed next, so too must a cryptographer interlace mathematical rigor with computer science acumen.
Moreover, the pursuit of a unified theory within cryptography presents a thrilling challenge for both mathematicians and computer scientists. With every breakthrough in algorithm design or mathematical proof, the potential for a more refined understanding strengthens. Consequently, the collaboration between these two disciplines is not merely advantageous; it is essential to foster innovation and ensure security in an increasingly digital world.
In summation, cryptography serves as a domain where the borders between applied mathematics and computer science blur, creating a fertile ground for intellectual exploration and application. This intricate relationship highlights the necessity of both fields to robustly secure and streamline communication in our modern age. The vibrancy of cryptography is propounded by its dependence on mathematical elegance, computational efficiency, and an unyielding pursuit of security. As technology advances, the dialogue between applied mathematics and computer science will only deepen, promising remarkable developments in the safeguarding of information that define our era.







Leave a Comment