Cryptography, often perceived as an esoteric domain governed purely by mathematical principles, possesses a layer of complexity that extends far beyond the confines of arithmetic and algebra. This perception elicits an intriguing examination into the symbiotic relationship between mathematics and statistics in cryptographic protocols, a nexus that engenders both sophisticated security mechanisms and nuanced vulnerabilities. By dissecting the intricate layers of cryptography, we unravel not only the fundamental principles that underpin secure communication but also the nuanced role of statistical analysis in reinforcing these cryptographic frameworks.
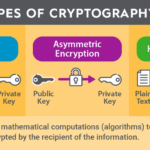
To commence, a foundational understanding of cryptographic mathematics is requisite. Cryptography relies heavily on algorithms that employ mathematical theories such as number theory, linear algebra, and abstract algebra. Cryptographic systems, whether asymmetric or symmetric, hinge on these mathematical constructs to secure data. For instance, the RSA algorithm—one of the earliest public-key cryptosystems—utilizes large prime numbers to create keys for encryption and decryption. The mathematical challenge posed by factorization of these large numbers is what fortifies the security of the RSA method, rendering it computationally arduous for unauthorized entities to decipher messages without the requisite key.
However, mathematical acumen alone does not suffice to encapsulate the entirety of cryptography. Herein lies the critical interjection of statistics. Statistical methodologies emerge as indispensable tools for assessing the randomness and unpredictability of cryptographic keys. The efficacy of cryptographic systems fundamentally hinges on their ability to resist various attacks, particularly those that exploit predictable patterns in key generation. Thus, statistics serve as a gatekeeper, evaluating the robustness of algorithms against potential vulnerabilities stemming from non-randomness.
Moreover, the concept of entropy becomes pivotal in the discourse on cryptographic strength. Entropy, in this context, quantifies the unpredictability or randomness of a cryptographic key. A key with high entropy is inherently more secure, resistant to brute-force attacks, which attempt to decipher encrypted data by exhaustive trial and error. The statistical distribution of key values plays a significant role in this aspect; an uneven distribution may lead to predictable patterns, markedly diminishing the level of security. Thus, statisticians and cryptographers are often embroiled in a collaborative effort to devise algorithms that maximize entropy through various means, such as chaotic systems or pseudo-random number generators.
The interplay between cryptography and statistics elucidates itself further when addressing the phenomenon of cryptanalysis. Cryptanalysis involves the study of methods for breaking encryption, thus revealing the intrinsic vulnerabilities of cryptographic systems. Here, statistical techniques are employed to glean insights into the encryption process, armed with the understanding that all encryption systems exhibit statistical properties. For example, frequency analysis, a classical technique employed in deciphering substitution ciphers, capitalizes on statistically analyzing the distribution of letters or patterns within a ciphertext to unveil the underlying plaintext. This demonstrates that sheer mathematical might can be subverted by keen statistical observation.
Furthermore, the advent of quantum computing heralds a new epoch in cryptographic discourse, one that profoundly illustrates the confluence of math and statistics. Quantum algorithms, such as Shor’s algorithm, threaten the very foundation of traditional cryptographic systems predicated on large prime factorization. Concurrently, statistical methods are being explored as a means to enhance post-quantum cryptography, which endeavors to secure cryptographic systems against the impending computational capabilities of quantum machines. The implications of such research highlight how statistical models disrupt and redefine established mathematical paradigms that have long governed cryptography.
This duality of mathematics and statistics is not simply an academic curiosity; it resonates with practical applications. In practice, secure communication employs a plethora of cryptographic protocols, ranging from HTTPS in secure web browsing to encryption standards like AES (Advanced Encryption Standard). These protocols meticulously blend mathematical constructs with statistical rigor to provide secure mechanisms for data transmission. Understanding this amalgamation is critical for developers and security practitioners who aim to craft resilient applications in an ever-evolving technological landscape.
Moreover, in evaluating the implications of this interplay, it is imperative to consider broader societal ramifications. Recognizing how statistical methodologies enhance cryptographic protocols informs policymakers about the importance of supporting research in both fields. As reliance on digital communication burgeons, safeguarding personal and sensitive information necessitates a robust understanding of the underlying frameworks that ensure data integrity and privacy. This awareness cultivates a culture of vigilance in digital interactions, empowering individuals to appreciate the complexities that cryptography encompasses.
In conclusion, the assertion that cryptography is exclusively a mathematical endeavor is an oversimplification that neglects the considerable contributions of statistical methodologies. The intricate tapestry of cryptographic science is woven from both mathematical rigor and statistical analysis, each element enhancing the robustness and effectiveness of secure communication protocols. This multifaceted relationship not only advances the technical capabilities of cryptography but also incites a deeper appreciation for the collaborative nature of these disciplines. As technology continues to advance, the intersection of mathematics and statistics will undeniably evolve, presenting new challenges and opportunities for cryptographers tasked with safeguarding our digital futures.






Leave a Comment