Introduction to RSA Encryption
In an age where digital communication is omnipresent, the imperative for secure methods of transmitting information cannot be overstated. One of the most pivotal innovations in this domain is the RSA encryption algorithm. Developed by Ron Rivest, Adi Shamir, and Leonard Adleman in 1977, RSA has become a cornerstone of public-key cryptography, enabling secure data exchange across the internet. Understanding its functioning and implications is fundamental for anyone venturing into the realm of cybersecurity.
1. The Unfathomable Base: Mathematical Foundations
To comprehend the mechanics of RSA, one must first delve into its mathematical underpinnings, which hinge primarily on the properties of prime numbers. The algorithm relies on the notion that while it is easy to multiply two large prime numbers, reversing the process — or factoring their product — becomes computationally strenuous as the numbers grow larger. This asymmetry forms the bedrock of RSA security, wherein the encryption (the multiplication of primes) is a straightforward operation, yet decryption (the factoring) remains a challenge shrouded in complexity.
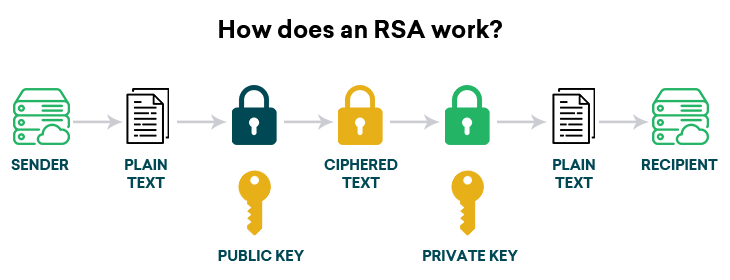
2. Generating Keys: The Dual Nature of Public and Private
Central to RSA is the concept of key pairs. Each user generates a unique public and private key through the following procedure:
- Select two large prime numbers: Let’s denote them as p and q. These primes should be sufficiently large (typically hundreds of digits) to ensure security.
- Calculate n: The product of p and q, referred to as n, is crucial as it is used in both the public and private keys. Its length, measured in bits, dictates the strength of the encryption.
- Determine the totient: This is calculated as (p-1)(q-1). This value is vital for computing the public and private exponents.
- Select the public exponent (e): Choose an integer e such that 1 < e < totient, with gcd(e, totient) = 1. Common choices for e are 3 or 65537, providing efficient encryption.
- Compute the private exponent (d): This is derived from the modular inverse of e modulo the totient. d is kept secret, ensuring only the key holder can decrypt messages.
The public key, comprising n and e, can be disseminated widely, while the private key d remains confidential, nestled safely with the user.
3. Encryption and Decryption: The Dance of Numbers
At the heart of RSA lies a simple yet profound mechanism for encrypting and decrypting messages. To encrypt a message m (represented as a number in the range of 0 to n-1), one employs the following formula:
C = me (mod n)
Where C is the ciphertext. Upon reception, the recipient can recover the original message by applying their private key d:
m = Cd (mod n)
This elegance of RSA lies in its ability to maintain the integrity of the plaintext while transforming it into a secure format for transit.
4. Practical Implementation: Integrating RSA into Systems
Transitioning from theoretical knowledge to practical applicability is a critical step. RSA is predominantly employed in various communication protocols, including but not limited to:
- Secure Socket Layer (SSL) and Transport Layer Security (TLS): These widely used protocols leverage RSA for establishing secure connections over the internet.
- Digital Signatures: RSA facilitates the authentication of documents, ensuring the integrity and origin of signatures in digital communications.
- Secure Email Transfer: PGP (Pretty Good Privacy) employs RSA for encrypting emails, safeguarding the privacy of correspondence.
Integrating RSA involves utilizing libraries and frameworks that encapsulate the complexities of key generation, encryption, and decryption. OpenSSL and Bouncy Castle are examples of such libraries, streamlining the implementation of RSA in diverse applications.
5. Strengths and Vulnerabilities: The Trade-offs
While RSA is robust, it is not without its vulnerabilities. Its security primarily hinges on the size of the keys. Current best practices advocate for key lengths of at least 2048 bits to mitigate risks posed by advancing computational power, particularly quantum computing. Notably, RSA is susceptible to specific attacks, such as timing attacks and chosen ciphertext attacks, which exploit weaknesses in how the algorithm is implemented rather than in its mathematical foundation.
6. A Glimpse into the Future: Beyond RSA
The incessant evolution of technology mandates that cryptographers remain vigilant. The rise of quantum computing threatens to unravel the security fabric of RSA, rendering it impotent against quantum algorithms like Shor’s algorithm, capable of factoring large integers efficiently. As a response, the cryptographic community is diligently exploring post-quantum cryptographic algorithms that promise to safeguard digital information in a quantum-dominated landscape.
Conclusion: Keeping the Enigma Alive
Ultimately, the RSA algorithm stands as a testament to the marriage of mathematics and technology, providing an enduring framework for web security. Its capability to enable secure communication fosters trust in digital platforms. Understanding and implementing RSA is not merely an academic endeavor; it is a necessity in a world increasingly reliant on secure data exchange. As cryptographic challenges continue to evolve, the fascination with RSA and its successors reflects humanity’s ceaseless quest for safety and privacy within the digital realm.







Leave a Comment