In the realm of cryptography, the generation and safekeeping of a private key in RSA encryption is akin to safeguarding the cornerstone of a formidable fortress. Visualize a grand castle, where the private key serves as the secret mechanism that unlocks the gates, permitting access to the innermost treasures. The significance of maintaining its integrity cannot be overstated. In this in-depth exploration, we will dissect the process of generating a private key in RSA and expound on various strategies to ensure its protection.
To embark on this cryptographic journey, one must understand the underlying principles of RSA (Rivest–Shamir–Adleman). RSA is a public-key cryptosystem that relies on the intricate dance of prime numbers. The security of this algorithm hinges upon the complexity of factoring large integers, making private keys virtuous guardians against unauthorized access.
The initial stage in the creation of an RSA private key entails the selection of two distinct prime numbers, typically denoted as ‘p’ and ‘q’. These numbers should be large enough to ensure robust security; a mere 2048 bits of key size is a prudent standard at the very least. In this context, prime numbers serve as the unyielding foundation upon which the RSA keys are constructed, much like sturdy stones that form the walls of our metaphorical castle.
Once the primes are chosen, it’s time to calculate the modulus, denoted as ‘n’, which is the product of ‘p’ and ‘q’ (n = p × q). This modulus forms the backbone of your RSA infrastructure, as it will be used in both the public and private keys. Following this, the Euler’s totient function, represented as φ(n), must be computed. This function is defined as φ(n) = (p-1) × (q-1), embodying the number of integers up to ‘n’ that are coprime to ‘n’. Understanding φ(n) is pivotal, as it plays a vital role in determining the private key.
The next step in this intricate process is the selection of an exponent ‘e’. This integer must satisfy two crucial criteria: it needs to be greater than 1 and less than φ(n), and it must be coprime to φ(n) itself. The choice of ‘e’ often gravitates towards 65537, a common exponent due to its optimal balance between speed and security, much like how an archer chooses a bow that delivers power without sacrificing precision.
With ‘p’, ‘q’, ‘n’, ‘e’, and φ(n) established, the challenge intensifies: calculating the private exponent ‘d’. This value is derived from the modular multiplicative inverse of ‘e’ modulo φ(n) (d ≡ e⁻¹ mod φ(n)). This mathematical venture requires a keen understanding of modular arithmetic and can often necessitate the use of the Extended Euclidean Algorithm, an invaluable tool for illuminating the path to ‘d’. Ultimately, this exponent, ‘d’, weaves together the fabric of your private key.
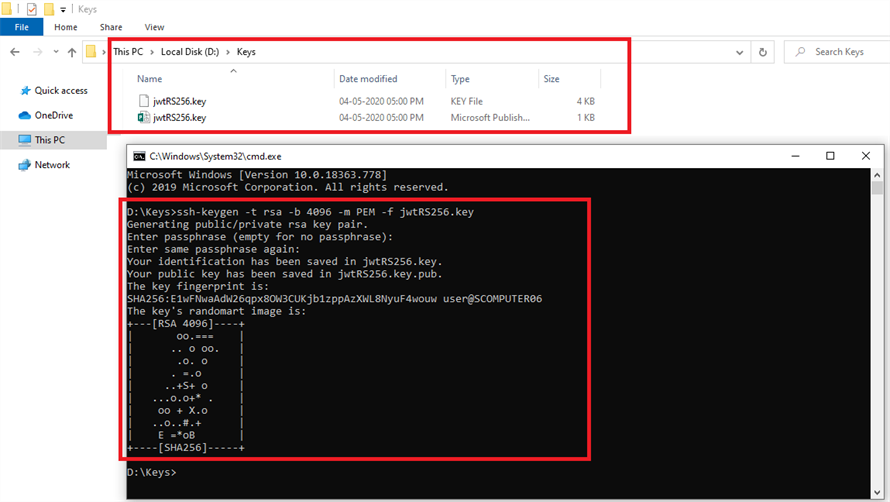
Upon completing these calculations, one possesses the private key, represented as the triplet (n, d), where ‘n’ is the modulus and ‘d’ is the private exponent. However, the journey does not conclude here. The paramount question remains: how does one ensure the safe custody of this invaluable key?
Consider your private key as a delicate artifact housed in a museum. Protection is of the essence. To fortify its sanctity, one must employ best practices including, but not limited to, the utilization of secure storage solutions. Hardware Security Modules (HSMs) are exemplary guardians, designed specifically for the storage and management of cryptographic keys. These devices offer both physical and logical security, creating an impenetrable bastion against theft and loss.
Similarly, employing strong passphrases is akin to fortifying the castle’s gates. A robust passphrase should comprise a mélange of uppercase and lowercase letters, numbers, and special characters. The objective is to generate a combination that remains both memorable and inscrutable to others, allowing only the rightful owner to retrieve the key.
It is equally vital to minimize exposure of the private key. Just as a vigilant monarch ensures that their castle gates are opened only for trusted allies, one should refrain from transmitting the key across potentially vulnerable channels. Instead, utilize encrypted storage for digital means, ensuring that the key is accessible solely under stringent access controls.
Another astute strategy involves the implementation of key rotation—a method that periodically replaces the private key with an entirely new one. Just as one might replace old steeds with new, healthier mounts, key rotation mitigates the risks associated with long-term exposure. Even if a key should be inadvertently compromised, the impact can be circumscribed, maintaining the integrity of the overall system.
Lastly, maintaining regular audits of your cryptographic practices is essential. Frequent evaluations not only heighten your awareness of potential vulnerabilities but also fortify your overall security architecture. Through continual assessment, one can identify weaknesses and implement corrective measures ahead of time, ensuring that the fortress remains impervious against evolving threats.
In closing, the generation of a private key in RSA encryption and its subsequent safeguarding can be likened to the meticulous construction and fortification of a stronghold. By understanding the intricate calculations required and embracing robust security practices, one can effectively protect against breaches and unauthorized access. Thus, by nurturing and safeguarding the cornerstone of your cryptographic fortress, you can ensure a safe passage through the complexities of digital communication and secure transactions.






Leave a Comment