Elliptic Curve Cryptography (ECC) has surged in prominence as digital security becomes increasingly essential. As technology proliferates, the demand for robust encryption mechanisms intensifies. ECC stands out for its efficacy, utilizing properties of elliptic curves over finite fields. This discussion will elucidate the intricacies of ECC, catered to those new to the subject while maintaining a depth that piques interest in its underlying mechanisms.
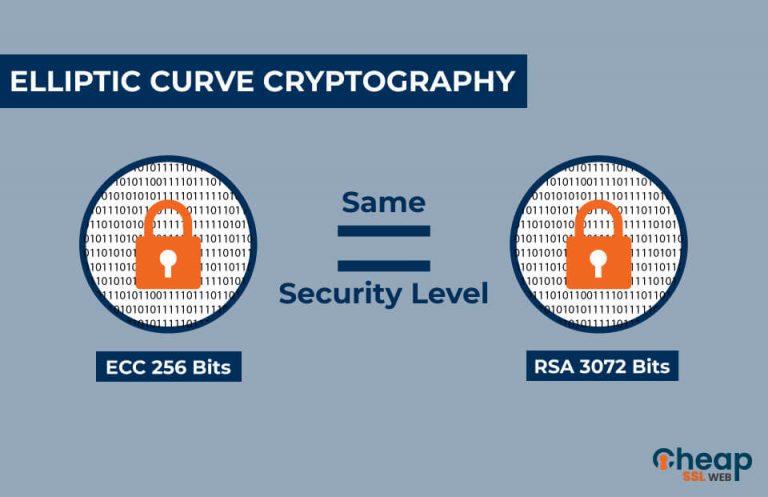
At its core, ECC fundamentally relates to the field of number theory, which underpins much of modern cryptographic practice. The allure of ECC stems from its ability to provide equivalent security to traditional cryptography, such as RSA, with significantly smaller key sizes. This characteristic translates to performance benefits in terms of speed and reduced computational overhead, making it particularly appealing for resource-constrained environments like mobile devices.
To comprehend ECC, it is crucial to first grasp the concept of elliptic curves. An elliptic curve is defined mathematically as the solutions to an equation of the form y² = x³ + ax + b, where ‘a’ and ‘b’ are constants that fulfill specific conditions to avoid singularities. These curves possess a unique geometric structure, manifesting as a smooth, continuous loop. The points on these curves, along with a defined “point at infinity,” form a group under a specific operation known as point addition.
The operation of point addition is central to ECC. When two points on the curve are added together, a third point can be derived. This operation involves drawing a line through the two points, determining where it intersects the curve, and reflecting that intersection across the x-axis. This resultant point is the sum of the two original points. Remarkably, this group structure allows for the development of cryptographic algorithms essential for secure communication.
One notable application of ECC is in key exchange protocols, such as the Elliptic Curve Diffie-Hellman (ECDH) scheme. This protocol allows two parties to securely derive a shared secret over a public channel. The elegance of ECDH lies in its use of a predefined base point on the curve. Each party generates a private key—a random number—and a corresponding public key derived from the base point using the point multiplication operation. This operation, despite its seeming simplicity, is computationally intensive and secures the public key exchange process.
Moreover, the security provided by ECC is predicated on the mathematical difficulty of the Elliptic Curve Discrete Logarithm Problem (ECDLP). To illustrate, while it is straightforward to take a point on the curve and multiply it by a scalar (the private key) to generate a new point (the public key), the reverse operation—deducing the scalar from the public key and base point—is computationally infeasible for sufficiently chosen curves. This aspect is what underlines the security of ECC; it is a one-way function that retains its complexity and challenge as computing power escalates.
The involvement of finite fields introduces another layer of sophistication. Typically, operations on elliptic curves occur over finite fields, which are mathematical structures consisting of a finite number of elements. The two most common types of finite fields used in ECC are prime fields and binary fields. Prime fields are denoted by the notation GF(p), where ‘p’ is a prime number, while binary fields are denoted GF(2^m), accommodating polynomial arithmetic. Each of these fields exhibits distinct operational characteristics that influence the efficiency and security of ECC implementations.
As is the case with any cryptographic method, the choice of elliptic curve parameters can significantly impact security. The National Institute of Standards and Technology (NIST) has delineated recommended curves, which are widely adopted for their rigorous security analysis. This recommendation underscores the importance of environments in which ECC is deployed, as selecting poorly-defined curves can render an implementation vulnerable to various attacks.
The steganography of ECC extends beyond merely securing communication; it forms the bedrock for digital signatures. Techniques such as the Elliptic Curve Digital Signature Algorithm (ECDSA) leverage the mathematical properties of elliptic curves to provide authentication and data integrity. Through the generation of a public-private key pair, ECDSA allows users to sign messages securely, with public verification mechanisms leveraging the same underlying group structure. The ramifications for secure transactions in e-commerce and digital identity assurance are profound.
As technology evolves, interest in ECC continues to burgeon, particularly with the advent of quantum computing. Quantum computers promise to upend traditional cryptographic schemes that rely on the difficulty of factorization or discrete logarithms. However, ECC’s resistance to such threats makes it an intriguing candidate for future post-quantum cryptography frameworks, warranting ongoing study and adaptation as cryptographic standards evolve.
In summation, the elegance of Elliptic Curve Cryptography lies in its mathematical foundation and its practical implications. Its ability to offer a high degree of security with smaller key sizes resonates with the demands of modern technological landscapes. As new generations of cryptographers explore the labyrinthine world of ECC, further discoveries will undoubtedly illuminate both its challenges and opportunities in the ceaseless pursuit of secure communication.






Leave a Comment