The Affine Cipher is a classic example of a monoalphabetic substitution cipher, which encodes messages through a linear transformation. This intriguing method combines the principles of modular arithmetic with the simplicity of basic substitution. While the Affine Cipher is relatively straightforward to implement when the encryption keys are known, decrypting it without the original key presents a substantial challenge. However, through systematic analysis and the application of certain techniques, one can uncover the hidden message even when the key is not at hand. This article delves into the processes and methods that allow for the decryption of an Affine Cipher without the initial cryptographic secrets.
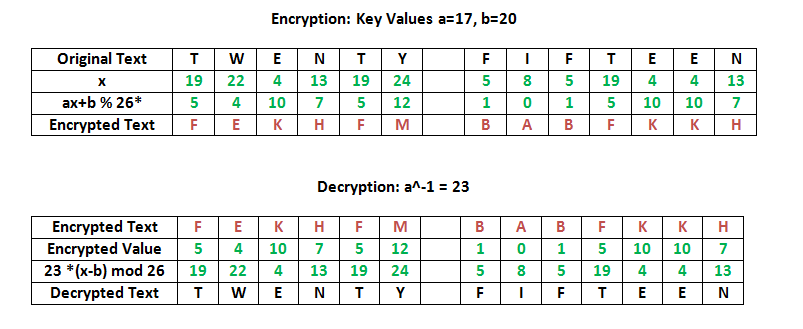
To begin with, it’s essential to understand the encryption mechanism employed in the Affine Cipher. The encryption is based on two key values, typically denoted as a and b. The mathematical formulation for encrypting a character P is represented as:
C = (aP + b) mod m
Here, C denotes the resultant ciphertext, m represents the size of the alphabet (commonly 26 for the English alphabet), P signifies the position of the plaintext character, and mod indicates the modulo operation to wrap around once the limits are exceeded. Consequently, the decryption process entails reverting this operation using the multiplicative inverse of a within the modulo space. However, to decrypt without the original keys, one must employ analytical techniques to unveil these values.
The first stage in the decryption endeavor involves frequency analysis. Since the Affine Cipher is a monoalphabetic cipher, it retains the frequency distribution of the plaintext characters in the ciphertext. English letters, for instance, exhibit characteristic frequency distributions—E is the most commonly used letter, followed by T, A, and so forth. By calculating the frequency of characters in the ciphertext, one can infer potential mappings to the plaintext characters. This step is crucial as it provides insights into the likely substitutions employed during encryption.
Next, one ought to identify possible letters that might correspond to the most frequent character in the ciphertext. For example, if the letter X appears the most frequently, it’s reasonable to hypothesize that this could correspond to E, the most common letter in the English language. By exploring various substitutions and observing how they affect the resulting text, one can begin constructing potential plaintext samples.
Furthermore, to refine this analysis, consider pairing frequency observations with digraph frequency analysis. The occurrence of letter pairs or digraphs in the English language creates additional patterns. For example, combinations like TH, HE, and IN are prevalent in English text. By analyzing the presence of such digraphs within the ciphertext, one can further narrow down possible mappings and enhance the accuracy of deduced substitutions.
While frequency analysis offers a substantial lead, the recovery of the keys remains incomplete without verifying potential a and b values. There are two key requirements for the value a in the Affine Cipher: it must be coprime with m (the alphabet size) and it cannot be zero. The integers that are coprime to 26 (the total letters in the English alphabet) are limited to {1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25}. By trying each of these values in the modular inverse criteria, one can mathematically test combinations of a and b values from previously established hypotheses generated through frequency analysis.
Once potential candidates for a and b are formulated, the next critical step is to systematically derive the decrypted text. By applying the formula:
P = a-1(C – b) mod m
where a-1 is the multiplicative inverse of a, one can substitute the guessed values into the equation. Validate each output by checking for coherent English phrases. Partial success in segments may suggest correct mappings while others require reevaluation of the frequencies and hypotheses regarding a and b.
Persistence, patience, and analytical reasoning are vital facets of this cryptographic unraveling. At times, challenges may arise when potential interpretations conflict or yield nonsensical outcomes. Therefore, it is prudent to maintain an iterative approach—continuously refining hypotheses based on newly discovered patterns and gleaned insights from segments of decrypted text.
In conclusion, decrypting an Affine Cipher without the original key may seem an arduous undertaking. Yet, through the lenses of frequency analysis, systematic hypothesis testing, and modular arithmetic, one’s understanding of cryptographic principles can yield significant breakthroughs. This process not only enhances the toolkit available for aspiring cryptanalysts but also intertwines the beauty of mathematical elegance with the intrigue of linguistics, thereby fostering a deeper appreciation for the complexities underlying seemingly simple ciphers.
Ultimately, the journey through this decryption process promises not merely the unlocking of hidden messages but also a newfound perspective on the artistry and enigma that reside within the realm of cryptography.







Leave a Comment