Public key cryptography, also known as asymmetric cryptography, is a complex yet essential aspect of securing digital communications. It hinges on a pair of keys: a public key, which can be shared with anyone, and a private key, which must be kept confidential. To grasp how these keys interrelate, one must delve into their fundamental operations, the cryptographic algorithms involved, and their applications across various digital landscapes.
At its core, public key cryptography utilizes mathematical functions to encrypt and decrypt messages. The most prevalent algorithms include RSA, Diffie-Hellman, and Elliptic Curve Cryptography (ECC). Each of these has its unique methodology and offers different levels of security and efficiency.
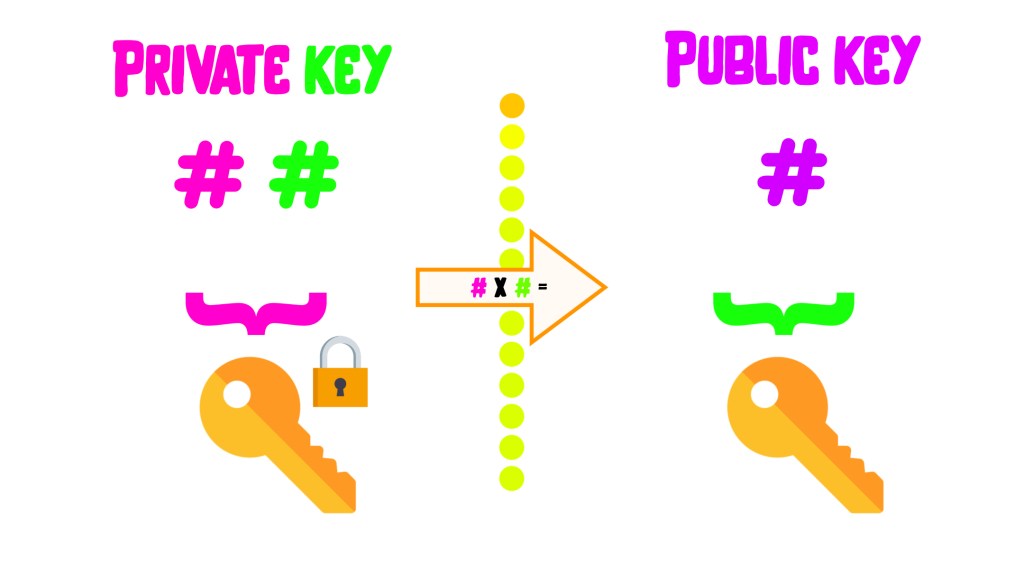
RSA, named after its inventors Rivest, Shamir, and Adleman, is one of the oldest and most widely used asymmetric algorithms. It employs large prime numbers as its foundation. The security is rooted in the difficulty of factoring the product of two large prime numbers. In RSA, the public key consists of two numbers: the modulus, which is the product of two large primes, and the public exponent, commonly set to 65537 due to its computational efficiency. The corresponding private key is generated using the extended Euclidean algorithm to find the modular inverse of the public exponent with respect to the totient of the modulus.
When a sender wishes to communicate securely, they encrypt their message using the recipient’s public key. The encrypted message, which appears as an incomprehensible string of characters, can only be deciphered by the holder of the private key. This mutual exclusivity ensures that even if a malicious actor intercepts the encrypted message, decryption remains impractical without the private key.
Another pivotal algorithm is Diffie-Hellman, primarily used for securely exchanging cryptographic keys over a public channel. Unlike RSA, Diffie-Hellman does not encrypt messages but rather facilitates the creation of a shared secret between two parties. Each party selects a private key and generates a public key from it, which is then exchanged. By performing calculations using the received public key and their own private key, both parties can derive the same shared secret. This secret can then be used to encrypt further communications using symmetric key algorithms.
Elliptic Curve Cryptography (ECC) has recently gained traction due to its robustness and efficiency. By employing the mathematics of elliptic curves over finite fields, ECC provides equivalent security to RSA with much smaller key sizes, considerably enhancing performance and scalability. For example, a 256-bit key in ECC is comparably secure to a 3072-bit RSA key, making ECC highly appealing for mobile and resource-constrained devices.
One imperative application of public key cryptography is in the realm of digital signatures. A digital signature is akin to a handwritten signature or a company seal, but it offers far more inherent security. To create a digital signature, the sender generates a hash of the message and then encrypts it with their private key. The resultant signature can then be attached to the original message. Upon receiving the message, the recipient can use the sender’s public key to decrypt the signature and compare the hash with their own calculated hash of the received message. If they match, it confirms both the integrity of the message and the identity of the sender.
Public key infrastructure (PKI) plays a vital role in managing public keys and their corresponding certificates. This system ensures that public keys are legitimate and have not been altered or misrepresented. Certificate Authorities (CAs) authenticate entities by issuing digital certificates that bind a public key to the identity of its owner. These certificates, which are digitally signed by the CA, facilitate trust in online transactions and communications, such as in HTTPS websites and secured email exchanges.
Moreover, as the digital landscape evolves, the importance of public and private keys extends beyond traditional communications. They play a crucial role in the advent of blockchain technology and cryptocurrencies. Here, public keys serve as wallet addresses, while private keys grant access to the associated funds. This paradigm shift signifies the critical need for robust key management practices, as loss or compromise of a private key results in irrevocable loss of assets.
Yet, the efficacy of public key cryptography is not immune to vulnerabilities. Quantum computing, while still in its infancy, poses significant threats to both RSA and ECC due to potential algorithms capable of solving the mathematical problems that underpin their security. This anticipated evolution in computing power could render conventional asymmetric methods obsolete, prompting researchers to explore post-quantum cryptographic solutions to counteract these looming challenges.
In conclusion, the functionalities of public and private keys underpin the security and integrity of contemporary digital communication. By understanding the mechanisms behind these cryptographic tools, one can appreciate their indispensable role in safeguarding data, preserving privacy, and establishing trust in a rapidly digitalizing world. As technology advances, continuous adaptations and innovations in cryptographic practices will remain imperative to counteract emerging threats and maintain robust defenses.







Leave a Comment