In an era where our digital lives are interconnected and increasingly vulnerable, the intricate web of cryptography emerges as a guardian at the gates of our virtual realm. It’s a discipline steeped in mathematical rigor, utilizing the profound principles of arithmetic, abstract algebra, and number theory to enhance our security. Just as a locksmith crafts a formidable key to secure a door, cryptographers employ algorithms and mathematical theory to forge keys that unlock and protect information. This intricate dance of mathematics and technology serves not only to secure data but also to establish trust in digital communications.
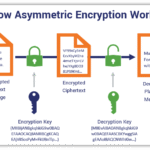
The cornerstone of cryptography is its mathematical underpinnings. At its core, cryptography relies on transformation—encoding information to obscure its original meaning. The process of encoding requires a function, a mathematical operation that manipulates data in ways that can only be reversed by those privy to the key. For instance, symmetric encryption algorithms use a single key for both encryption and decryption, while asymmetric encryption employs a pair of keys: a public key, which can be shared freely, and a private key, kept confidential by the owner. This duality not only creates barriers for potential eavesdroppers but also invokes intriguing metaphors of trust and secret-keeping within the digital landscape.
One of the most celebrated examples of such cryptographic systems is the RSA algorithm, named after its illustrious creators Rivest, Shamir, and Adleman. The algorithm generates keys based on the mathematical difficulty of factoring large prime numbers. Imagine attempting to locate a needle in a haystack where the needle composition can substantially alter but remains distinctly unique—this illustrates the challenge posed to would-be attackers. The inherent complexity of breaking down large composite numbers is what renders RSA both formidable and intriguing. As computational power increases, the quest for larger primes becomes a race against time for cryptographers, making the art of encryption not only a matter of mathematics but also a continuous evolutionary process.
Moreover, the power of cryptography extends beyond simple encryption. Hash functions epitomize an essential aspect of digital security. Think of a hash function as a digital fingerprint, a unique identifier that encodes data of any size into a fixed length. It serves two primary functions: ensuring data integrity and enabling quick data retrieval. An example of this is the SHA-256 algorithm, part of the Secure Hash Algorithm family. It transforms input data into a seemingly random string of hexadecimal characters. In the realm of blockchain, this property is pivotal, ensuring that any alteration in the original data would yield a drastically different hash, thus safeguarding against tampering. The mathematical elegance of hash functions connects deeply with notions of identity and verification.
The proliferation of online communication and transactions necessitates a robust framework of security protocols, with Transport Layer Security (TLS) setting the standard for secure communications over networks. At the heart of TLS lies the negotiation of keys through a public key infrastructure (PKI). It’s akin to an elaborate dance where participants must validate one another before exchanging secrets. Through the interwoven strands of certificates and digital signatures, trust is established, assuring users that they are dealing with legitimate parties. The calculations involved rely on elliptic curve cryptography, a more advanced alternative that offers the same level of security with shorter key lengths, streamlining the efficiency of secure connections.
Equally fascinating is the role of the Diffie-Hellman key exchange, which revolutionized the way secure keys are shared. It represents a paradigm shift akin to finding a secret tunnel that allows two parties to exchange information without ever meeting. By using the properties of modular arithmetic along with a shared base and a prime number, two individuals can create a common secret in plain sight without ever revealing it to potential observers. This mathematical ingenuity is testimony to the evolving nature of cryptography, where the emphasis is not just on creating impenetrable locks but also on establishing clever mechanisms for secure collaboration.
As we navigate through this digital labyrinth, the importance of quantum resistance emerges. With the advent of quantum computing—an evolution that challenges classical cryptographic schemes—mathematicians are hard at work developing quantum-resistant algorithms. The potential power of quantum computers can render traditional encryption vulnerable, leading to a renaissance in cryptographic research. Here, the mathematical elegance of lattice-based cryptography, among others, provides a tantalizing glimpse into a future where security adapts to technological advancements.
In conclusion, the intersection of cryptography and mathematics is a testament to human ingenuity. Each algorithm, function, and theorem serves as a cog in a much larger machine—a machine designed to protect our most sensitive information. The elegance contained within complex mathematical formulas not only secures our data but also fosters trust in our digital interactions. As we continue to traverse the increasingly intricate landscapes of the digital world, the preservation of mathematical integrity within cryptography will be paramount in maintaining the sanctity of our virtual lives. Thus, the dialogue between mathematics and security is not merely a technical necessity; it is an ongoing narrative that weaves itself into the very fabric of our technological existence.








Leave a Comment