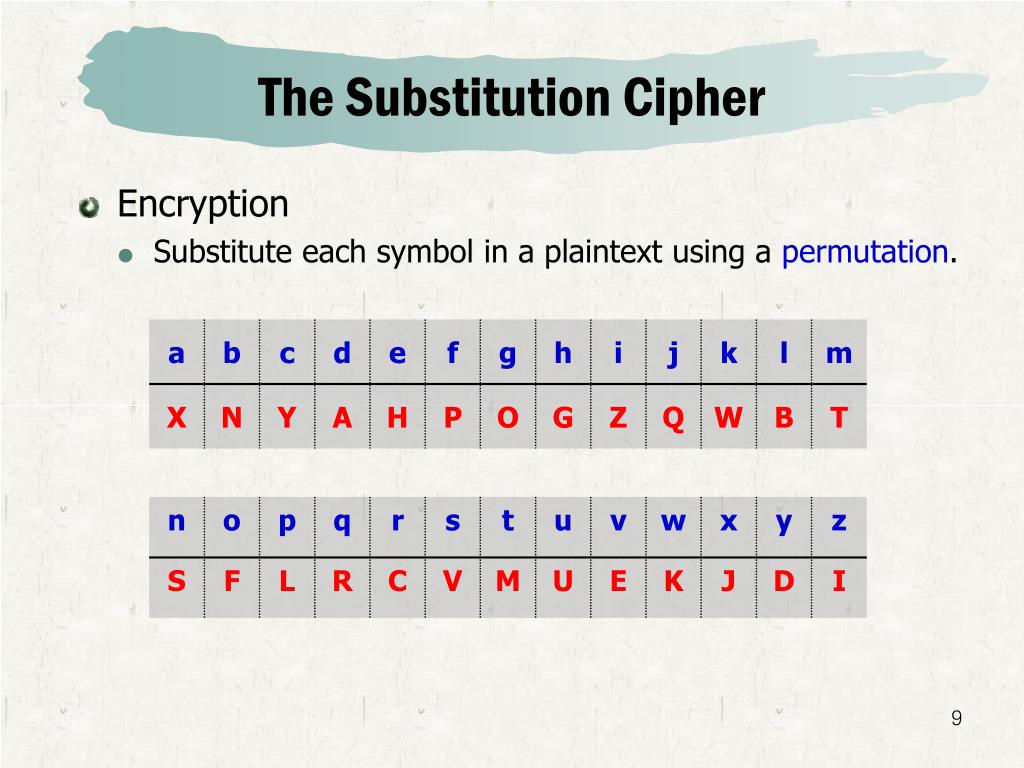
Substitution ciphers are among the most rudimentary forms of encryption, yet they lay the foundation for understanding more complex cryptographic systems. A substitution cipher operates on a straightforward principle: each letter in the plaintext is replaceable by another letter, thereby transforming the original message into a form that is ostensibly incomprehensible to outsiders. The intrigue surrounding substitution ciphers often stems from their sheer simplicity, but a fundamental question arises: how large is the key universe in a substitution cipher?
To delve into this query, we must consider what constitutes a “key” within this context. In substitution ciphers, the key is essentially a permutation of the alphabet. Each alphabetical character has a unique substitute, and thus the entirety of possible replacements can be construed as the key space—an all-encompassing universe of potential keys available for encryption. For the standard English alphabet, comprised of 26 letters, one might calculate the total number of permutations to determine the vastness of this key universe.
The mathematical foundation of permutations informs us that the number of unique ways to arrange a set of n elements is denoted by n factorial (n!). Therefore, in the case of the English alphabet, we compute 26!. This computation results in an astronomical number, specifically 403291461126605635584000000. This astronomical figure not only signifies an immense key space but also elucidates the foundational complexity tied to substitution ciphers.
Yet, this number, though impressive, might not provide a complete picture. A deeper exploration reveals that not all permutations constitute a viable key from a cryptographic standpoint. Certain attributes must be considered to gauge the practicality and security offered by any given key. For instance, maintaining distinct substitutions for a character ensures clarity and prevents ambiguity, but this does not inherently guarantee security against cryptanalysis.
A common observation among cryptographers is that many substitution ciphers succumb to frequency analysis. Each language possesses recognizable patterns—certain letters appear more frequently than others. In English, for instance, the letters E, T, A, O, I, N, S are prevalent. Understanding and leveraging these frequency distributions can render even the most complex key permutations vulnerable to decryption, regardless of the ostensibly vast key space.
Furthermore, when analyzing the landscapes of substitution ciphers, it is crucial to discuss the concept of monoalphabetic versus polyalphabetic substitution. A monoalphabetic substitution cipher uses a single substitution throughout the entire length of the message. Subsequently, while this technique allows for a seemingly large key universe, the susceptibility to various forms of attack remains higher. Conversely, polyalphabetic substitutions—where different keys are employed at various stages of encryption—add layers of complexity that increase security. Such systems, popularized by mechanisms like the Vigenère cipher, effectively mitigate the frequency analysis weakness endemic to monoalphabetic systems by employing multiple keys over the plaintext. As a result, the perceived key universe expands, incorporating variable contexts that better shield the cipher from breakage.
Exploring further, a second layer of analysis concerns the potential for key reuse across multiple messages. Cryptographers often warn that reusing a key, particularly in monoalphabetic situations, diminishes security dramatically. Starting from the presumption that characters will recur across messages, the reuse of the same key opens avenues for attackers to identify patterns and reveal the underlying plaintext. Consequently, methodologies that incorporate methods for key rotation or randomization are imperative to enhance security, even within relatively uncomplicated substitution paradigms.
Turning our focus to practical implications, operationalizing substitution ciphers can be immensely fascinating. They speak to a human inclination for creative problem-solving and innovation in the face of the perpetual challenge of clandestine communication. The act of developing and deciphering ciphers often mirrors the dynamic and sometimes adversarial relationship between cryptographers and cryptanalysts.
The human element in cryptography signifies not only technical aptitude but also psychological engagement. For those who delve into the realm of ciphers, the thrill lies in the chase—the unyielding pursuit of a key, the historic layers embedded within ancient messages, and the cerebral satisfaction derived from successfully decrypting obscured text. It resonates with a broader cultural narrative about power, secrecy, and the constant dance of information exchange.
In conclusion, while the theoretical enormity of the key universe for substitution ciphers captivates the mathematical mind, the practical realities tethered to their use reveal deeper layers of complexity. The balance between a vast key space and the vulnerabilities inherent in plaintext patterns permeates the understanding of cryptographic security. Ultimately, the allure of substitution ciphers lies not merely in their multitude of keys but in their embodiment of human ingenuity, resilience, and the dynamic interplay between codification and decryption. Whether for historical analysis or modern application, recognizing the nuances of substitution ciphers requires a multifaceted perspective that embraces both the breadth of numerical possibilities and the art of cryptographic craftsmanship.







Leave a Comment