In the labyrinth of modern cryptography, where strength and elegance converge, elliptic curves emerge as intricate yet formidable guardians of digital information. These mathematically rich entities not only serve a purpose but also weave a narrative that is at once fascinating and profoundly essential to the digital age. This article delves into the enthralling relationship between elliptic curves and cryptography, illuminating their unique synergy and profound implications.
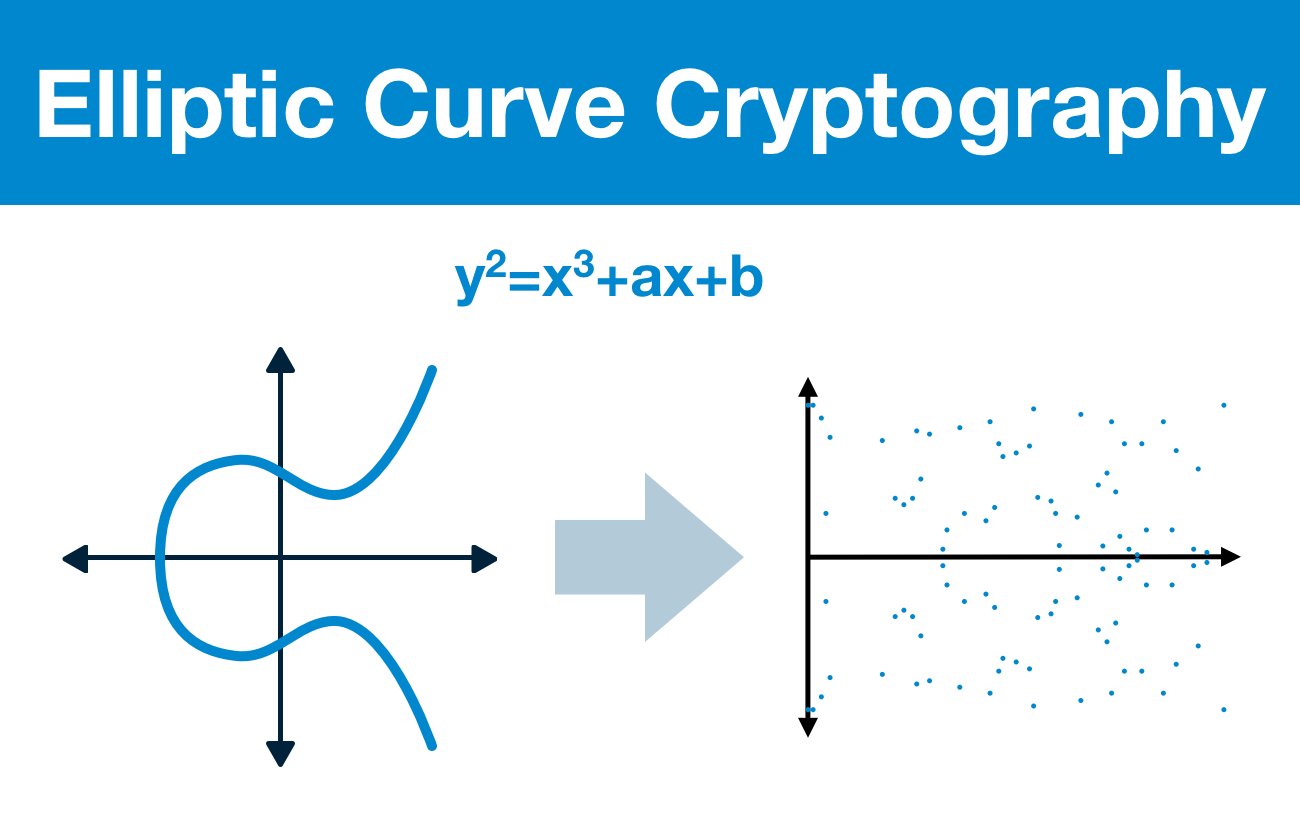
At the heart of this discussion lies the elliptic curve itself, a structure defined within the realm of algebraic geometry. Each curve is epitomized by a specific equation, typically of the form y² = x³ + ax + b, wherein the coefficients a and b are constants. These curves can be visualized as smooth, continuous shapes that twist and turn, creating an enchanting landscape on a coordinate plane. The points on these curves form a group under a defined operation, which, although simple in essence, gives rise to complex interactions that are the backbone of elliptic curve cryptography (ECC).
The allure of elliptic curves beckons not merely through their aesthetic appeal but also through their mathematical properties, which offer unparalleled advantages in the field of cryptography. Unlike traditional methods such as RSA, which depend on the difficulty of factoring large integers, elliptic curve cryptography rests upon the elliptic curve discrete logarithm problem. This problem is significantly harder to solve, which allows for shorter key lengths while maintaining an equivalent level of security. In this way, elliptic curves epitomize efficiency; they deliver robust security with a diminutive footprint, much like a compact fortress that can withstand the might of an army.
This inherent efficiency is particularly advantageous in an era that necessitates swift communication and limited computational resources. The mobile devices and Internet of Things (IoT) applications that populate our contemporary landscape demand encryption techniques that conserve power and bandwidth. Elliptic curve cryptography accommodates this necessity flawlessly, providing a secure framework that can be tessellated into the fabric of these devices without overburdening them. The efficiency of ECC thus transforms it into a linchpin for modern encryptions.
Furthermore, niched applications have also arisen, with elliptic curve techniques being employed in blockchain technologies and cryptocurrencies. The explosive growth of these digital assets has ushered in a newfound appreciation for cryptographic security. In this milieu, the utilization of elliptic curves enhances transaction security, ensuring that the keys governing ownership are both unbreakable and efficient. Herein lies a metaphorical symbiosis: as the cryptocurrency ecosystem burgeons, elliptic curves yield complications that serve to fortify its foundations.
Yet, the interplay between elliptic curves and cryptography extends beyond mere performance metrics. There is a poetic simplicity inherent in their mathematical relationships. Each point on an elliptic curve can be seen as a pixel in a vast digital canvas, where every transaction, every message, can be encapsulated within the magic of these curves. This metaphor enriches the imagination and inspires a deeper appreciation of the underlying principles that safeguard our virtual identities.
The journey from the abstract realm of mathematics to real-world applications unveils layers of complexity that draw one in further. This transition is marked by the implementation of various ECC protocols, each tailored to fulfill specific requirements. The Elliptic Curve Digital Signature Algorithm (ECDSA), for example, is a widely used manifestation of ECC designed to authenticate messages through the creation of unique digital signatures. ECDSA blends security with a measure of flexibility, allowing it to thrive across diverse computing environments.
Moreover, when one examines the deployment of elliptic curves in secure communications protocols, such as Transport Layer Security (TLS), the picture becomes clearer. As data oscillates between servers and clients, ECC acts as a cryptographic handshake, a gesture of trust inherent in the design of secure connections. This handshake establishes the foundation on which data integrity is assured, akin to a knight donning armor before embarking on a quest.
However, the trajectory of elliptic curve cryptography is not devoid of challenges. As computational power continues to surge, the cryptographic community’s gaze turns towards potential vulnerabilities. The rise of quantum computing casts a shadow over existing algorithms, including ECC. The Shor’s algorithm, for instance, presents a theoretical threat capable of undermining the very principles that the security of ECC rests upon. Consequently, adaptive measures are sought, with discussions surrounding post-quantum cryptography gathering momentum.
This paradoxical dance between security and obsolescence invites contemplation: while elliptic curves now represent the pinnacle of cryptographic sophistication, they must perpetually evolve to counter emerging threats. This cyclical necessity for innovation intensifies the allure of the elliptic curve, painting it not only as a pillar of contemporary cryptography but also as a dynamic entity that perpetually seeks equilibrium in an ever-shifting landscape.
In summation, the union of elliptic curves and cryptography constitutes a multifaceted symbiosis, where mathematical elegance meets functional necessity. The narrative woven by elliptic curves extends beyond the confines of cryptography, inviting reflections on efficiency, security, and the ever-present specter of advancement. As digital interactions become increasingly woven into the fabric of our daily lives, the role of elliptic curves as bastions of security grows ever more pivotal. Indeed, in this age of information, elliptic curves and cryptography are, unequivocally, a match made in the intricate and beautiful world of mathematics.






Leave a Comment