In the ever-evolving landscape of cryptography, elliptic curves have emerged as a cornerstone of modern secure communication. By 2025, heeding the whispers of their complexities and advantages demands a deeper understanding of elliptic curve secrets. Are you ready to untangle the enigma that encapsulates elliptic curves? This intricate thread of mathematics serves as the foundation for a multitude of encryption protocols, promising security in an age where digital integrity is paramount. However, can we confidently ascertain the implications of their widespread adoption?
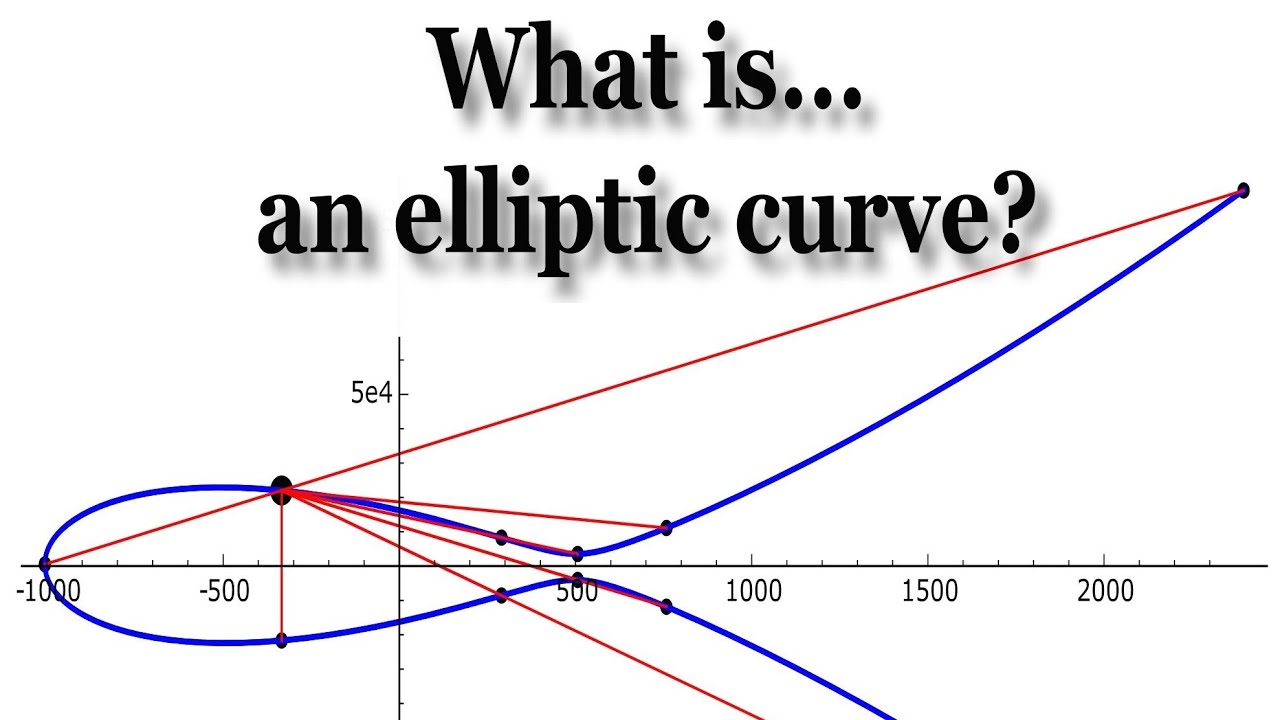
To commence this exploration, we must first define what an elliptic curve is. Mathematically, an elliptic curve can be expressed as a smooth, projective algebraic curve defined by a specific equation. Most commonly, this equation takes the form y² = x³ + ax + b, where a and b are selected constants that satisfy certain conditions. Herein lies the beauty: each point on the curve is a coordinate pair (x, y) that yields a valid equation, lending itself to a rich structure governed by group laws.
The utility of elliptic curves emanates from their mathematical properties. Cryptographic systems exploit these curves through what is known as Elliptic Curve Cryptography (ECC). The challenge arises not in the operational efficiency, but in the inherent complexity of using these curves. What makes ECC an attractive alternative to traditional cryptographic methods, such as RSA, is its ability to provide akin levels of security with significantly smaller key sizes. For instance, a 256-bit key using ECC is equivalent to a staggering 3072-bit key in RSA. Why does this matter? Less computational load results in faster processing times and lower power consumption—traits invaluable in a world increasingly reliant on mobile devices.
However, with great power comes great responsibility. The advantages of ECC invite a range of challenges. One pressing concern encompasses the potential vulnerability to quantum computing advancements. Quantum algorithms, particularly Shor’s algorithm, threaten to unravel the security mechanisms that underpin traditional cryptographic systems. As researchers probe the depths of quantum resistance, one must ponder: will the resilience of elliptic curves withstand the quantum tide? This looming specter necessitates proactive contemplation on the future of encryption methodologies.
In light of these advancements, let’s delve into the practical implications of elliptic curve technologies. Enterprise applications are abundant, from securing online transactions to facilitating secure messaging platforms. Notably, the implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA) has garnered prominence in blockchain technology, enhancing the veracity and immutability of transactions. Conversely, developers aiming to implement ECC must navigate a lexicon of complexities—issues such as curve selection, parameter generation, and potential side-channel attacks present formidable challenges that require a comprehensive understanding of the underlying mathematics.
The conversation about elliptic curves also extends into the realm of regulatory compliance. As various industries grapple with data privacy laws, including GDPR and CCPA, the resilience of cryptographic systems becomes a focal point. Thus, elliptic curves not only bolster security but also serve as a mechanism to adhere to compliance mandates. Organizations must weigh the adoption of ECC thoughtfully, as improper implementation could lead to costly ramifications both financially and reputationally.
Moreover, the proliferation of open-source cryptographic libraries has spurred an increased curiosity regarding elliptic curves. For developers, familiarity with these libraries—such as OpenSSL and Libgcrypt—can be a double-edged sword. While access to high-quality implementations eases the development process, it also exposes projects to external vulnerabilities. What is the balance between convenience and security in a world rife with potential third-party risks? Navigating this landscape requires a vigilant eye and a robust security posture.
As the horizon stretches into 2025, the potential vitality of elliptic curves presents new possibilities. With the advent of post-quantum cryptography, researchers are exploring novel curve constructions designed to withstand quantum attacks. Questions arise: will organizations pivot to these new paradigms? Are current elliptic curves sufficient, or are they merely holding ground until a more resilient option rises to the forefront? The confluence of mathematical ingenuity and cryptographic application will undoubtedly dictate the trajectory of secure communication methods.
In conclusion, the secrets of elliptic curves are profound and multifaceted. While they afford the promise of security through efficient encryption algorithms, the challenges posed by evolving technological landscapes cannot be overlooked. As stakeholders prepare for the encroaching digital age of 2025, delving into elliptic curve secrets will yield a deeper comprehension of both their potential and limitations. Engaging with this enchanting world not only cultivates knowledge, but it also breeds innovation—an essential trait for any entity hoping to thrive in the complex dance of cryptography. Will you join in the quest to unravel the secrets tucked within elliptic curves and embrace the future they herald? The challenge lies before you, and the rewards could be substantial.







Leave a Comment