Imagine you have two friends who each have a secret they want to share with one another, but they do not want anyone else to eavesdrop on their conversation. How can they exchange secret messages securely without the worry of prying eyes? This playful inquiry introduces us to the fascinating world of Elliptic Curve Cryptography (ECC), a powerful technique that underpins modern digital security.
At its core, ECC is a form of public-key cryptography that leverages the properties of elliptic curves over finite fields. These curves are mathematically intriguing objects that help simplify complex operations, thereby facilitating secure communication. To better understand these concepts, let’s embark on a comprehensive exploration of ECC, aiming to dissect its mechanics without inducing confusion.
First, let’s break down what elliptic curves are. A standard elliptic curve can be expressed in the form of the equation y² = x³ + ax + b, where a and b are constants that determine the specific shape and characteristics of the curve. These curves come with a unique point at infinity, making them somewhat resemble the loops of a giant rollercoaster—an infinite journey in a finite space.
What sets elliptic curves apart from other mathematical constructs is their application in cryptography. The mathematical properties of these curves enable the creation of complex yet efficient algorithms that can protect our information with a high degree of security. But, how does one traverse from familiar integers to the more abstract world of elliptic curves? The challenge lies in grasping the addition of points on these curves.
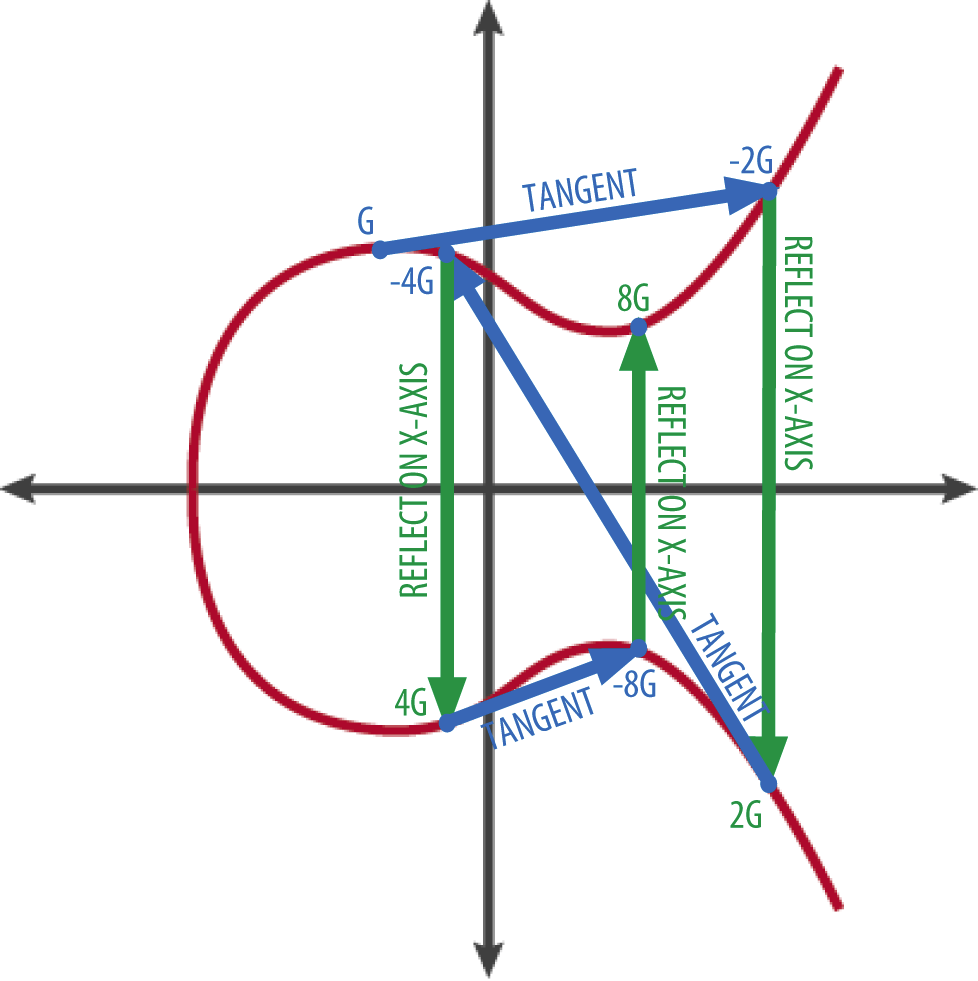
When we think about adding numbers, we follow straightforward arithmetic rules. In the realm of elliptic curves, the process takes on a new dimension. Each point on the curve can be visualized as an ordered pair (x, y). The addition of two points entails drawing a line through them, observing where it intersects the curve again. This intersection point, when reflected across the x-axis, yields the resultant point of addition. This operation—although geometric and somewhat whimsical—carries the heavy lifting for the security protocols that utilize ECC.
Now, one may wonder why elliptic curves are preferable to traditional methods, such as RSA (Rivest–Shamir–Adleman). The answer lies in the efficiency of computations. ECC provides the same level of security as RSA but with significantly smaller key sizes. For instance, a 256-bit key in ECC can offer comparable security to a 3072-bit key in RSA. This reduction in size translates to faster computations and lower resource consumption, making ECC particularly appealing for devices with limited processing power, such as smartphones and Internet of Things (IoT) devices.
But let’s consider a practical illustration. Say Alice wants to send a secure message to Bob. Using ECC, Alice generates a pair of keys: a public key and a private key. The public key is like an open mailbox: anyone can drop a message in but only the owner—the person with the private key—can retrieve it. Bob engages in a similar process, ensuring that their interaction remains confidential. This public-private key system underpins a vast array of modern digital communication, from secure email to cryptocurrency transactions.
One might ask, is the mathematics behind ECC solely theoretical? Quite the opposite, as the principles are actively employed in securing our digital landscape. Cryptographic protocols like TLS (Transport Layer Security) rely heavily on elliptic curves to establish secure connections over the internet. The transportation of sensitive data is anchored in the robustness offered by ECC, rendering it a cornerstone of cybersecurity.
However, one faces potential hurdles when attempting to implement ECC. One significant challenge is the risk of vulnerabilities found in poorly implemented cryptographic algorithms. For ECC to function as intended, attention must be paid to the underlying parameters and random number generation processes to prevent susceptibility to attacks. Malicious entities may leverage flaws within an implementation to gain unauthorized access, compromising the integrity of the communication.
For those intrigued by the intricate workings of ECC, there is a plethora of resources available. From academic papers delving into the complexities of elliptic curves to online courses designed to demystify the mathematical underpinnings, enthusiasts can cultivate their knowledge. Additionally, numerous libraries and programming tools exist to facilitate the practical use of ECC in software applications, empowering developers to enhance security protocols with relative ease.
As we conclude this journey through the realm of elliptic curves and their cryptographic applications, the landscape is both rich and complex. While the mathematics may seem daunting, the principles behind ECC are foundational to maintaining privacy in our increasingly interconnected world. As illustrated through the analogy of Alice and Bob, the beauty of ECC lies in its ability to provide robust security without convoluting the process for either party.
In light of the ever-evolving threats to digital security, embracing the elegance of elliptic curve-based systems is not simply an academic exercise but a necessary step towards safeguarding our confidential communications. Can you imagine the possibilities? What further advancements might emerge as we delve deeper into the world of elliptic curves?







Leave a Comment