Elliptic Curve Cryptography (ECC) stands as a hallmark of modern cryptographic techniques, offering robust security while employing smaller key sizes compared to traditional methods such as RSA. This characteristic not only enhances performance but also significantly conserves computational resources, making ECC particularly well-suited for devices with limited processing power. Despite its technical complexity, the allure of ECC lies in its underlying mathematical intricacies and the elegant curves that constitute its framework.
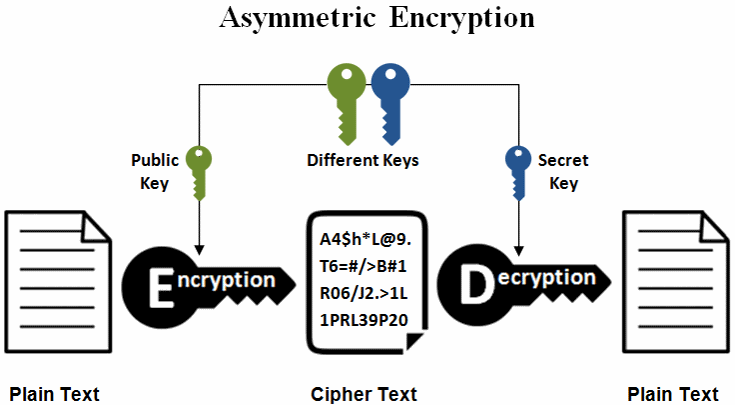
The essence of ECC revolves around elliptic curves, which are defined by equations that illustrate a smooth, continuous set of points. These curves exhibit distinct mathematical properties, most notably their closed group structure. The addition of points on an elliptic curve follows a set of rules that, at first glance, appear esoteric. However, they serve as the foundation for generating a public and private key pair. The private key remains secret, while the public key can be freely distributed. This dynamic engenders a secure method of encryption and digital signatures that is impervious to common cryptographic attacks.
One of the prevailing observations regarding ECC is that, unlike traditional encryption methods, it can achieve the same level of security with significantly smaller keys. To illustrate, a 256-bit key in ECC can provide security equivalent to a 3072-bit key in RSA. This disparity arises from the mathematical complexity inherent in the elliptic curve discrete logarithm problem (ECDLP), which remains computationally infeasible to solve even using advanced techniques. Consequently, the efficiency and security profile of ECC have ignited widespread interest among developers and security architects alike.
The analytical nature of ECC promotes a deeper appreciation for its applications, particularly in an era where data breaches and cyber threats proliferate. As digital communications increasingly rely on secure encryption methods, ECC emerges as a compelling candidate for securing sensitive transactions, particularly in online banking, e-commerce, and secure messaging. Its capacity for establishing secure channels efficiently makes it a pivotal component in future technological advancements.
To grasp the intricacies of ECC fully, one must familiarize oneself with the concept of elliptic curves over finite fields. These curves come in various forms, each possessing unique attributes that influence their use in cryptography. The incorporation of curves like secp256k1, widely recognized in the realm of cryptocurrency, exemplifies how specific parameters can foster substantial security while facilitating quick computations.
Moreover, ECC’s flexibility allows it to be employed in various protocols. For instance, the renowned Transport Layer Security (TLS) handshake can adopt ECC to negotiate cryptographic parameters efficiently. By harnessing elliptic curve key exchange protocols, parties can establish secure communication channels, enhancing the overall security posture of digital interactions.
Yet, what fuels this fascination with ECC extends beyond mere efficiency and security. The cryptographic community is drawn to the elegance of the mathematics involved. The interplay between algebra, geometry, and number theory in elliptic curves reveals a rich tapestry of insights and techniques that resonate with those who appreciate the beauty of mathematics. In some respects, the study of ECC transcends practical application, beckoning enthusiasts to explore the theoretical frameworks that underpin its efficacy.
Common criticisms of ECC often surface regarding the perceived complexity of implementation, which can lead to vulnerabilities if not executed correctly. Erroneous parameter selection, improper key generation procedures, or inadequate randomness can compromise security. Nevertheless, when implemented with care, ECC provides a fortification against a multitude of cyber threats, serving as a bastion of security in an increasingly perilous digital landscape.
As we navigate these treacherous waters, the robustness of ECC underscores the necessity for continued research and innovation in cryptographic practices. One cannot ignore the interdisciplinary nature of cryptography; advancements in computer science, mathematics, and cybersecurity converge to address pressing challenges. This collaborative effort fosters a culture of perpetual learning, with ECC at the forefront, challenging cryptographers to refine their methodologies continually.
Furthermore, with the emergence of quantum computing, a looming specter threatens existing cryptographic paradigms. The advent of such technology could render traditional encryption methods obsolete. Yet, ECC presents promising avenues for quantum-resistant alternatives, particularly through the development of post-quantum algorithms. This prospect only adds to the intrigue surrounding elliptic curves and their potential roles in a post-quantum world.
In conclusion, the fascination with ECC stems not solely from its ability to provide robust security but also from the underlying mathematical beauty and potential for future resilience. As cyber threats evolve, embracing the complexities of elliptic curve cryptography becomes paramount. By understanding the mechanics of curves, keys, and the intricate dance of mathematical principles, individuals and organizations can craft effective cyber shields that safeguard our digital future. ECC is not merely a method; it is a powerful demonstration of how mathematics can inform and enhance security in a technologically driven world.






Leave a Comment