In the intricate tapestry of modern cryptography, the Diffie-Hellman key exchange stands out as a pivotal innovation. Introduced in 1976 by Whitfield Diffie and Martin Hellman, this groundbreaking method revolutionized the way secure communications can be established over potentially insecure channels. At its core, the Diffie-Hellman key exchange facilitates the creation of a shared secret between parties, enabling them to communicate securely in a manner that was previously unfathomable.
The essence of the Diffie-Hellman protocol lies in its utilization of mathematical principles, particularly those related to modular arithmetic and exponentiation. To comprehend its impact, one must first grasp the fundamental concept of public and private keys. In traditional cryptographic systems, keys are used to encrypt and decrypt messages. The intrigue of the Diffie-Hellman approach is that it allows two parties to jointly create a secret key without the need to exchange the actual key itself, mitigating the risks of interception experienced in conventional methods.
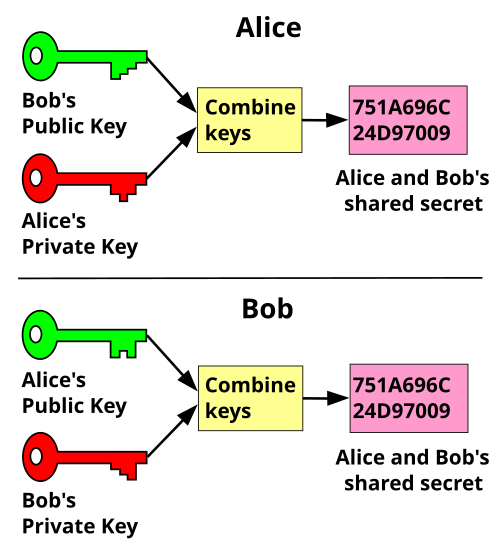
The operation begins with two parties, commonly referred to as Alice and Bob, who wish to establish a secure communication channel. They agree upon two public numbers: a prime number ( p ) and a base ( g ). These parameters do not need to remain confidential; they can be disseminated openly. The choice of a sufficiently large prime number is crucial, as it directly influences the algorithm’s resistance against brute-force attacks.
Once the public parameters are established, each party generates their own private key. For simplicity, assume Alice selects a private key ( a ), while Bob chooses ( b ). These private keys are never shared with anyone, preserving their confidentiality. The strength of the Diffie-Hellman protocol is rooted in the complexity of computing discrete logarithms, which serves as the foundational security underpinning this exchange.
Alice then computes the value ( A = g^a mod p ) and sends it to Bob. Simultaneously, Bob computes ( B = g^b mod p ) and sends it to Alice. By leveraging the mathematical properties of exponentiation, both parties can compute the shared secret key independently. Alice calculates ( s = B^a mod p ), while Bob computes ( s = A^b mod p ). In both cases, the result is identical, yielding a shared secret ( s ) that remains impervious to eavesdroppers.
This ingenious method relies heavily on the difficulty of certain mathematical problems. The discrete logarithm problem, which requires deducing the exponent when provided with a base and its resultant modulus, is computationally arduous. This one-way function forms the crux of Diffie-Hellman’s security, rendering the derived shared secret secure against potential adversaries who might intercept the public values ( A ) and ( B ).
While the Diffie-Hellman key exchange significantly enhances secure communications, it is not without its limitations and vulnerabilities. One primary concern lies in the absence of authentication. An attacker could potentially launch a man-in-the-middle (MitM) attack by impersonating one of the communicating parties, thus establishing a separate secure channel with each participant. This vulnerability underscores the necessity of integrating additional security measures, such as digital signatures or public key infrastructures (PKIs), to ensure authenticity alongside confidentiality.
Intriguingly, the Diffie-Hellman mechanism can also be expanded into ephemeral key exchanges, where new key pairs are generated for each session. This practice enhances security by reducing the risk of compromise associated with long-term keys. By utilizing ephemeral keys, even if one session’s key were to be exposed, it would not jeopardize the integrity of future communications, thus preserving long-term confidentiality.
Moreover, the versatility of the Diffie-Hellman key exchange has allowed it to become a cornerstone in various cryptographic protocols and systems, including Secure Sockets Layer (SSL) and Transport Layer Security (TLS). These protocols, essential for securing web traffic, rely on Diffie-Hellman not only to establish secure connections but also to facilitate the exchange of symmetric keys that are utilized for encrypting subsequent communications.
It is crucial to stay attuned to advancements in cryptography as the landscape continually evolves with growing computational power and emerging threats. As quantum computing advances, the efficacy of traditional cryptographic algorithms may be undermined. Researchers are exploring post-quantum cryptography to develop resilient systems that can withstand the capabilities of quantum attacks. The Diffie-Hellman key exchange, while secure today, must be re-evaluated and potentially adapted to ensure its long-term viability in a quantum-dominated future.
To conclude, the Diffie-Hellman key exchange encapsulates the ingenuity of cryptographic innovation. By enabling secure key sharing without direct transmission of sensitive information, it exemplifies the principles of secrecy and security within the digital realm. Understanding this protocol, along with its strengths and limitations, invites a broader conversation about the nature of trust, privacy, and the safeguarding of information in an increasingly interconnected world. The ongoing evolution of cryptographic methods will undoubtedly fuel curiosity and prompt critical discourse on how we navigate the complexities of secure communication in the digital age.







Leave a Comment