The discourse on public key cryptography often leads to a pivotal inquiry: Can the RSA private key be reconstructed from its public counterpart? To address this question, one must delve into the intricacies of the RSA algorithm itself. RSA, standing for Rivest-Shamir-Adleman, is a cornerstone of modern cryptography, enabling secure data transmission over insecure channels. The algorithm relies on the mathematical properties of large prime numbers, making it robust against various types of attacks.
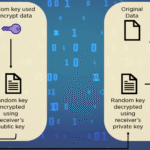
In RSA, two keys work in tandem: the public key, which is made widely available, and the private key, which is kept confidential. The public key is comprised of two components, (n) and (e), where (n) is the product of two distinct prime numbers, (p) and (q), and (e) is an integer less than (phi(n))—Euler’s totient of (n). The private key, on the other hand, is derived from (n) and (d), where (d) is the modular multiplicative inverse of (e) modulo (phi(n)). This complex interplay of mathematical functions is what theoretically shields the private key from discovery through the public key.
At the heart of the puzzle lies the factorization of large integers. While the public key is easily computable, reversing the process—deriving (p) and (q) from (n)—is the crux of the challenge. The security of RSA hinges upon the fact that while multiplication of large primes is computationally trivial, the inverse operation, factorization, remains exponentially complex as the key size increases. Current computational methods lack efficiency in factorizing products of sufficiently large primes, thus rendering the private key secure under normal circumstances.
However, the ultimate question surfaces: is it truly impossible to reconstruct the private key from the public key? The answer is not as straightforward as one might hope. Cryptographers have demonstrated that the risk of key reconstruction increases with the development of more sophisticated algorithms and advances in computational power. The burgeoning field of quantum computing, for instance, poses a formidable threat. Quantum algorithms, like Shor’s algorithm, have the potential to factorize large integers efficiently, undermining the very foundation of RSA’s security.
Furthermore, the choice of key length plays a crucial role. Current standards recommend a key length of at least 2048 bits to safeguard against potential future threats. Shorter keys can be subject to brute-force attacks or targeted factorization attempts using highly optimized algorithms. Therefore, it is imperative for individuals and organizations to assess their risk exposure and choose RSA key lengths judiciously in light of ongoing advancements within the computational landscape.
In addition to the implications of computational power, one should not overlook vulnerabilities arising from implementation flaws. Cryptographic libraries must be meticulously scrutinized for bugs and weaknesses, as even small errors in the design or execution of RSA can expose private keys to decryption risks. For instance, inadequate randomness in key generation can lead to situations where public keys become more predictable, thus increasing the likelihood of key reconstruction attacks.
The historical backdrop of cryptography reveals that technical enhancements often follow in the wake of significant theoretical breakthroughs. As researchers continue to explore new methodologies, the cryptographic community is urged not to remain complacent. Staying abreast of innovations in information security, particularly in the realm of public key infrastructure, requires an ethos of adaptability and continual reassessment of the tools at one’s disposal.
Moreover, the necessity of public awareness is paramount. Non-experts must grasp the relevance of cryptographic practices, especially in an era where digital transactions dominate everyday life. Ultimately, enhancing understanding empowers individuals to make informed decisions about the privacy and security of their digital communications.
In conclusion, while the RSA private key cannot be feasibly reconstructed from the public key under current normal circumstances, this notion is not devoid of caveats. The security of RSA relies heavily on computational complexity, where large prime factorization remains computationally challenging. However, as technology evolves, so too do the risks associated with public key cryptography. The specter of quantum computing looms large, promising a paradigm shift in how we conceptualize encryption and decryption. Thus, vigilance in cryptographic practices and proactive measures against emerging threats is not merely advantageous, but essential. The realm of cybersecurity is dynamic; what remains salient today may be rendered obsolete tomorrow. Cultivating curiosity and maintaining a critical perspective are vital for navigating this murky yet crucial domain of information security.






Leave a Comment