Quantum cryptography is at the forefront of secure communications, leveraging the principles of quantum mechanics to protect information. Within this domain, the conversation often revolves around the potential for an eavesdropper, whom we will refer to as Eve. This analysis explores the question of whether Eve can ‘win’ in the context of quantum cryptographic protocols, particularly focusing on various scenarios that echo familiar guessing games. The scenario not only illustrates the intense competition between secure communication and eavesdropping but also elucidates fundamental principles of quantum mechanics.
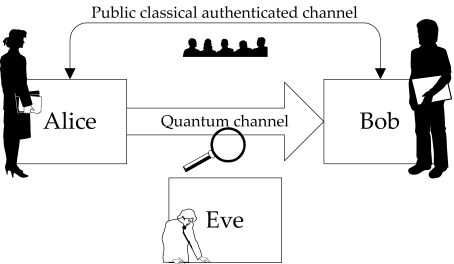
At the heart of quantum cryptography lies the concept of quantum key distribution (QKD). This process allows two parties, traditionally named Alice and Bob, to share a secret key securely, even in the presence of a potential eavesdropper, Eve. Central to this discussion is the Bell theorem, which contemplates the implications of entangled particles. The distribution of entangled quantum states implies that any intrusion by Eve can be detected, as measuring quantum states alters the original data. But can Eve exploit the system to guess the key correctly?
One of the foundational techniques utilized in QKD is the BB84 protocol, which employs four non-orthogonal states of polarization. Each time Alice prepares a photon in one of the four states to send to Bob, Eve faces an inherent challenge. When she attempts to intercept and measure these photons, she is forced to choose between the basis for measurement. This choice generates disturbances in the system, revealing her presence. Thus, while Eve might be able to acquire some information about the key, her ability to deduce the complete, accurate key is fundamentally hindered by the laws of quantum mechanics.
However, suppose Eve decides to adopt a strategy akin to educated guessing. In a traditional guessing game—like determining the color of a hidden object or the answer to a riddle—she might employ statistics to inform her choices. In the quantum realm, each photon transmitted carries an intrinsic element of unpredictability, making it challenging for Eve to formulate a reliable strategy based solely on past measurements. The difficulty is accentuated when we introduce noise within the communication channel, which further muddies the clarity of the transmitted data.
The strategy of using eavesdropping techniques, such as photon number splitting (PNS), adds another layer of complexity to this analysis. With PNS, Eve can theoretically capture some photons from the quantum channel while allowing the rest to pass to Bob. However, again, this method comes with limitations. Alice and Bob can detect significant discrepancies in the key, signaling whether Eve has meddled. Thus, Eve’s capacity to guess correctly diminishes when faced with the robust fault-tolerance and detection mechanisms embedded within QKD protocols.
Furthermore, there’s a distinction between short-term interventions versus long-term strategies by Eve. In a traditional guessing game, consistent play can lead to eventual success. However, in the realm of quantum cryptography, the ephemeral nature of quantum states—such as the principle of superposition—presents an obstacle. When Eve captures a photon, she effectively collapses its state, causing a change that can be sensed by Alice and Bob. Therefore, this argument emphasizes that Eve’s intermittent guessing strategies are less likely to yield fruitful results.
Beyond the mechanics of photons lies the philosophical discussion of trust in quantum cryptography. While Alice and Bob can guarantee mutual trust through the framework of QKD, there remains an inherent uncertainty regarding Eve’s capabilities. Some researchers propose the existence of future, potentially less constrained quantum algorithms that could augment Eve’s guessing prowess. This evolving discourse challenges cryptographers to innovate continuously, staying ahead of potential vulnerabilities.
Moreover, the introduction of more complex protocols—such as the Quantum Digital Signatures—offers Alice and Bob additional tools to reinforce the integrity of their communication. By implementing such intricate systems, the traditional guessing game is transformed into a more strategic interplay where Eve might find her guessing game increasingly futile. The continued evolution of these cryptographic systems illustrates the dynamic nature of the field, as new solutions emerge to tackle evolving threats.
It is important to consider the implications of these developments. While Eve’s ability to win in this guessing game of quantum cryptography remains largely restricted, future advancements in both quantum computing and eavesdropping tactics could present unprecedented challenges. The cat-and-mouse game that characterizes cryptography compels continuous vigilance among cryptographers to safeguard information. Nevertheless, the robust framework provided by quantum mechanics underpins a level of security that instills confidence in users.
Ultimately, in pondering the question, “Can Eve win?” it becomes clear that the intrinsic properties of quantum mechanics provide formidable barriers against eavesdropping. The guessing games played by Eve are riddled with uncertainty, reflecting an intricate interplay of strategy and physics. As Alice and Bob explore the frontiers of secure communication, they do so with a profound awareness of the dynamism inherent in technology and the continuous evolution of adversarial tactics. Thus, while Eve may not outright win the game, the landscape of quantum cryptography ensures a perpetual reinforcement of security as new strategies and protocols are unveiled.







Leave a Comment