Implementing RSA encryption in real life can seem like an enterprise reserved for the technocrats of the digital age. However, its underlying principles are accessible and can be operationalized in various sectors, from personal communications to secure transactions. This guide delineates the process of RSA implementation in an uncomplicated yet rigorous manner, ensuring clarity amidst complexity.
At its core, RSA (Rivest-Shamir-Adleman) is a public-key cryptography system that enables secure data transmission. The fascination surrounding RSA revolves not solely around its practical utility but the mathematical elegance and security it embodies. To truly appreciate RSA, one must comprehend its mechanics, which hinge on the fundamental principles of number theory. This is where the journey begins—understanding the components necessary for RSA’s implementation.
1. Understanding RSA’s Foundations
RSA is predicated on the properties of large prime numbers and their multiplicative inverses. At the heart of RSA encryption lies the following steps:
- Choosing Two Prime Numbers: Begin with the selection of two distinct large primes, ( p ) and ( q ). The security of RSA rests largely on the difficulty of factoring the product of these two large primes.
- Computing the Modulus: Calculate ( n = p times q ). This modulus ( n ) is used in both the public and private keys.
- Calculating the Totient: Determine ( phi(n) = (p-1)(q-1) ). This totient is critical in deriving the keys.
2. Generating RSA Keys
The next pivotal phase involves generating a public and private key pair:
- Selecting the Public Exponent: Choose an integer ( e ) such that ( 1 < e < phi(n) ) and ( e ) is coprime to ( phi(n) ). A common choice for ( e ) is 65537, given its properties favorable for efficient computation.
- Calculating the Private Exponent: Compute ( d ), the modular multiplicative inverse of ( e ) modulo ( phi(n) ). This ensures that ( ed equiv 1 (text{mod} phi(n)) ).
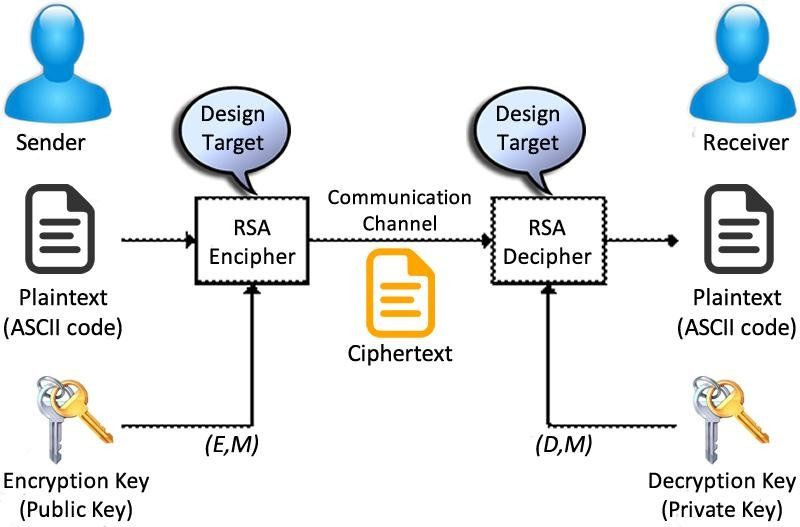
- Constructing the Key Pairs: The public key consists of the pair ( (e, n) ), while the private key comprises ( (d, n) ). These keys enable encryption and decryption procedures, respectively.
3. Encryption and Decryption Process
With the keys established, one can proceed to the primary functions of RSA—encryption and decryption:
- Encrypting Messages: To encrypt a plaintext message ( m ), convert ( m ) to an integer in the range ( 0 ) to ( n-1 ). The ciphertext ( c ) can be computed using the formula: c ≡ me (mod n).
- Decrypting Messages: Upon receiving the ciphertext ( c ), the recipient can decrypt it by computing m ≡ cd (mod n) using their private key. This reconstructs the original message ( m ).
4. Practical Applications of RSA
The versatility of RSA encryption extends beyond theoretical exercises. Its applications permeate numerous facets of modern technology:
- Secure Communication: RSA underpins the security algorithms used in websites via HTTPS, safeguarding credit card transactions and user data.
- Digital Signatures: RSA can authenticate individuals by generating digital signatures, providing both integrity and non-repudiation.
- Data Encryption: From emails to secure data storage, RSA facilitates the encryption of sensitive data, ensuring confidentiality.
5. Challenges and Future Considerations
Despite its robustness, RSA is not without limitations. As computational power escalates, so do the strategies to undermine RSA’s security.
- Key Length: The length of keys is paramount; keys must be sufficiently long to mitigate the risk of factorization attacks. Current recommendations suggest key lengths of at least 2048 bits.
- Quantum Computing: With the advent of quantum computing, traditional RSA encryption faces existential threats as algorithms like Shor’s algorithm can factor large integers exponentially faster than classical algorithms.
In conclusion, the implementation of RSA in real-life applications is both a laudable endeavor and an intricate challenge. By grasping the foundational elements and processes of RSA—from prime selection to key generation and encryption—you can leverage its capabilities to enhance data security in various digital landscapes. The elegance of RSA is not merely in its mathematical precision but in its ability to foster trust in our increasingly interconnected world.






Leave a Comment