In the realm of modern mathematics, two fields of study, graph theory and cryptography, may seem to exist in parallel universes. Yet, a closer examination reveals that they intersect in ways that promise to reshape the landscape of secure communications. This unlikely union beckons to those intrigued by the profound intricacies of data protection and theoretical constructs.
Graph theory, a branch of discrete mathematics, revolves around the study of graphs—collections of vertices and edges that model pairwise relations between objects. As an elegant framework, it provides a powerful means to represent networks in various forms, from social interactions to communication systems. Cryptography, on the other hand, is the art of encoding messages to ensure confidentiality and integrity. At first glance, these domains occupy distinct territories; however, their amalgamation reveals a plethora of innovative applications.
To grasp the connection between these two fields, one must delve into the fundamental properties of graphs. A graph consists of nodes interconnected by edges, which can represent anything from people (in social media networks) to routers (in computer networks). The versatility of graphs enables cryptographers to model the relationships between entities in numerous ways. Imagine a labyrinthine network where each node signifies a user and every edge symbolizes the flow of information. Visualizing data in this manner facilitates a deeper understanding of potential vulnerabilities and strengths within a communication framework.
The melding of graph theory and cryptography might sound abstract, but it yields tangible developments. One such innovation is the use of graph-based cryptographic algorithms. A striking example is the construction of public-key cryptosystems derived from the complexity of certain graphs. Traditional cryptographic methods often rely on number theory, yet graph-based systems open up a novel approach that could prove more resilient against emerging threats, particularly those posed by quantum computing.
As cryptography evolves, there is increasing concern over the robustness of classical algorithms such as RSA and ECC (Elliptic Curve Cryptography). These systems, while currently secure, have vulnerabilities that could be exploited by quantum algorithms. Herein lies the promise of graph-based cryptography. By leveraging the intricate structures of graphs, particularly through techniques like lattice-based cryptography, cryptographers can create algorithms that may be resistant to the onslaught of quantum threats.
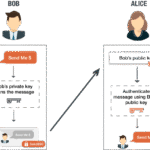
Extending beyond security, graph-based cryptography facilitates efficient communication protocols. Consider the potential of using graphs to streamline the distribution of keys in a network. In scenarios where numerous entities must engage in secure communication, the task of key distribution often becomes a bottleneck. Graph theory offers protocols, such as peer-to-peer key exchanges, that enhance efficiency. Through a series of structured interactions modeled by graphs, nodes can share keys without the need for a central authority, thereby reducing vulnerability to interception.
Moreover, the synergy between graph theory and cryptography can be observed in the realm of consensus protocols. These protocols are essential in distributed systems, such as blockchains, where multiple parties must agree on transaction validation. Graph-based structures can enhance the efficiency and reliability of these protocols, ensuring that all participants reach consensus without compromising security. By creating an immutable ledger where transactions are represented as a series of interconnected nodes, the integrity of data is secured against potential tampering.
The intersection of these two fields is also fertile ground for exploring privacy-preserving technologies. By applying graph theory to construct sophisticated anonymization techniques, it is possible to obscure user identities within networks while still retaining data utility. Techniques drawn from graph theory can facilitate the design of privacy-preserving algorithms that allow data sharing across federated systems without revealing sensitive information, thus maintaining user confidentiality while enabling collaboration.
Despite the immense potential that arises from the merger of graph theory and cryptography, challenges persist. Cryptographers must grapple with the inherent complexity of graph structures, as computations can quickly become intractable with larger graphs. Furthermore, the field is still in the nascent stages of developing practical applications that fully exploit these theoretical advancements. Yet, researchers remain undeterred, driven by the belief that the benefits far outweigh the obstacles.
As we journey through this thrilling interdisciplinary terrain, the confluence of graph theory and cryptography not only enriches our understanding of secure communication but also opens the door to a plethora of applications across diverse domains. From enhancing cybersecurity measures to empowering decentralized systems, the insights garnered from graph structures provide a fresh perspective on age-old problems.
In conclusion, the intersection of graph theory and cryptography serves as a testament to the endless possibilities that arise when seemingly disparate fields converge. As this relationship deepens, it fosters an environment ripe for innovation and creativity. The surprising connection between these two domains invites further inquiry, encouraging researchers and practitioners alike to continue exploring the intricacies of their interaction. In a world increasingly defined by data and connectivity, the implications of this relationship are profound, potentially heralding a new era of secure communication.






Leave a Comment