In the pantheon of cryptographic techniques, Hill’s Cipher stands as a fascinating yet largely obsolete method that dates back to the early 20th century. Developed by mathematician Lester S. Hill in 1929, it represented an innovative leap in the realm of polygraphic ciphers by utilizing linear algebra to encrypt messages. However, as the field of cryptography has evolved, the limitations of Hill’s Cipher have become increasingly apparent. This exploration delves into the perennial constraints of Hill’s Cipher and elucidates why it remains seldom employed in contemporary applications.
1. The Mathematical Foundation: Matrix Operations
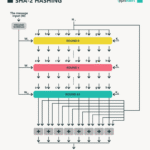
At the heart of Hill’s Cipher lies a fundamental dependence on linear algebra, particularly matrix multiplication. The encryption process begins with the conversion of plaintext into numerical vectors, allowing matrices to transform these numbers into ciphertext. For a simple illustration, consider a 2×2 matrix used against 2-dimensional plaintext vectors. While this might seem revolutionary in the 1920s, the reliance on matrix inversion introduces complications, particularly as the key size increases.
Thus, the mathematical elegance of Hill’s Cipher, initially a strong selling point, now presents significant problems. The requirement that the key matrix must be invertible mod n constrains potential key choices and renders the method vulnerable when practitioners fail to heed this requisition.
2. Vulnerability to Frequency Analysis
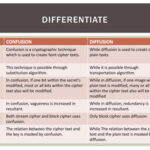
One of the critical weaknesses of Hill’s Cipher is its susceptibility to frequency analysis, a cryptanalytic technique prevalent since the days of Caesar. Given that the ciphertext is a product of linear combinations of plaintext characters, patterns emerge with repeated usage of the key matrix. Cryptanalysts can exploit these patterns to establish relationships between variables. For instance, if two ciphertext letters correspond to the same pair or a single matrix operation, their plaintext equivalents might become apparent.
In an era increasingly dominated by digital communication, the rapid ability to analyze and decipher encrypted messages using computational resources further erodes the security Hills’s Cipher initially seemed to promise. This is a pressing concern given that modern encryption demands an amplified level of sophistication that Hill’s methodology simply cannot provide.
3. Limitations of Key Space
The key space in Hill’s Cipher is both its strength and its downfall. While, theoretically, any invertible matrix can serve as a key, practical limitations restrict these choices. The number of possible keys is significantly smaller compared to more advanced systems like RSA or AES. As key lengths increase, the number of possible keys diminishes due to the constraints imposed by matrix arithmetic and modular conditions.
This limited key space not only reduces the complexity that can be achieved but also encourages the use of shorter keys. Shorter keys imply a higher probability of successful brute-force attacks, especially in an era where computational power is surging exponentially. Consequently, this restriction becomes a critical impediment when juxtaposed against the relentless march of technology.
4. Inefficiency in Digital Communication
Hill’s Cipher, with its matrix manipulations, lacks efficiency in both encryption and decryption processes. In practical applications, the substantial computational overhead introduced by matrix calculations can hinder real-time communication. In our current landscape, where speed is of the essence, such inefficiencies equate to an unacceptable burden. The rise of streamlined algorithms that prioritize efficiency has rendered Hill’s Cipher quaint at best.
Modern communication systems often require rapid bulk encryption, especially in secure transactions or data transfers. Other encryption methods, such as symmetric and asymmetric key algorithms, have emerged to meet these demands, virtually sidelining matrix-based ciphers like Hill’s.
5. The Rise of Sophisticated Algorithms
As cryptography continues to evolve, the emergence of sophisticated algorithms with enhanced security features has made classical ciphers like Hill’s increasingly redundant. Algorithms such as AES (Advanced Encryption Standard) and RSA (Rivest-Shamir-Adleman) utilize complex mathematical principles on a scale that dwarf the simplicity of Hill’s system. AES provides not just a larger key space but also employs multiple rounds of processing, effectively thwarting most known attack vectors.
The intricate internal structure of modern encryption algorithms, combined with their resilient nature against various types of cryptanalytic attacks, renders Hill’s Cipher nearly anachronistic. As cryptology advances, the simplicity and vulnerabilities of Hill’s method have relegated it to a role primarily in academic contexts, more as a learning tool than a viable encryption technique.
6. Conclusion: The Obsolescence of a Classic
In conclusion, while Hill’s Cipher occupies an essential position in the historical narrative of cryptography, its practicality in the contemporary world is severely limited. The vulnerabilities to frequency analysis, constrained key spaces, inefficiencies in operation, and the sheer dominance of more advanced encryption algorithms overshadow its mathematical elegance. While Hill’s method may serve as a foundational concept within cryptography classes, its application in real-world scenarios remains minimal. As we navigate an increasingly digital future, understanding these shortcomings is crucial for appreciating the evolution and ongoing innovations in the field of encryption.







Leave a Comment