Elliptic curves, a sophisticated and elegant mathematical structure, have become a cornerstone of modern cryptography. Their properties offer unique advantages that can potentially revolutionize the way we approach secure communications and data protection in an increasingly digital world. This exploration delves into the intricacies of elliptic curves, the fundamental principles governing them, their applications in cryptography, and the implications they hold for the future of secure information exchange.
Understanding Elliptic Curves
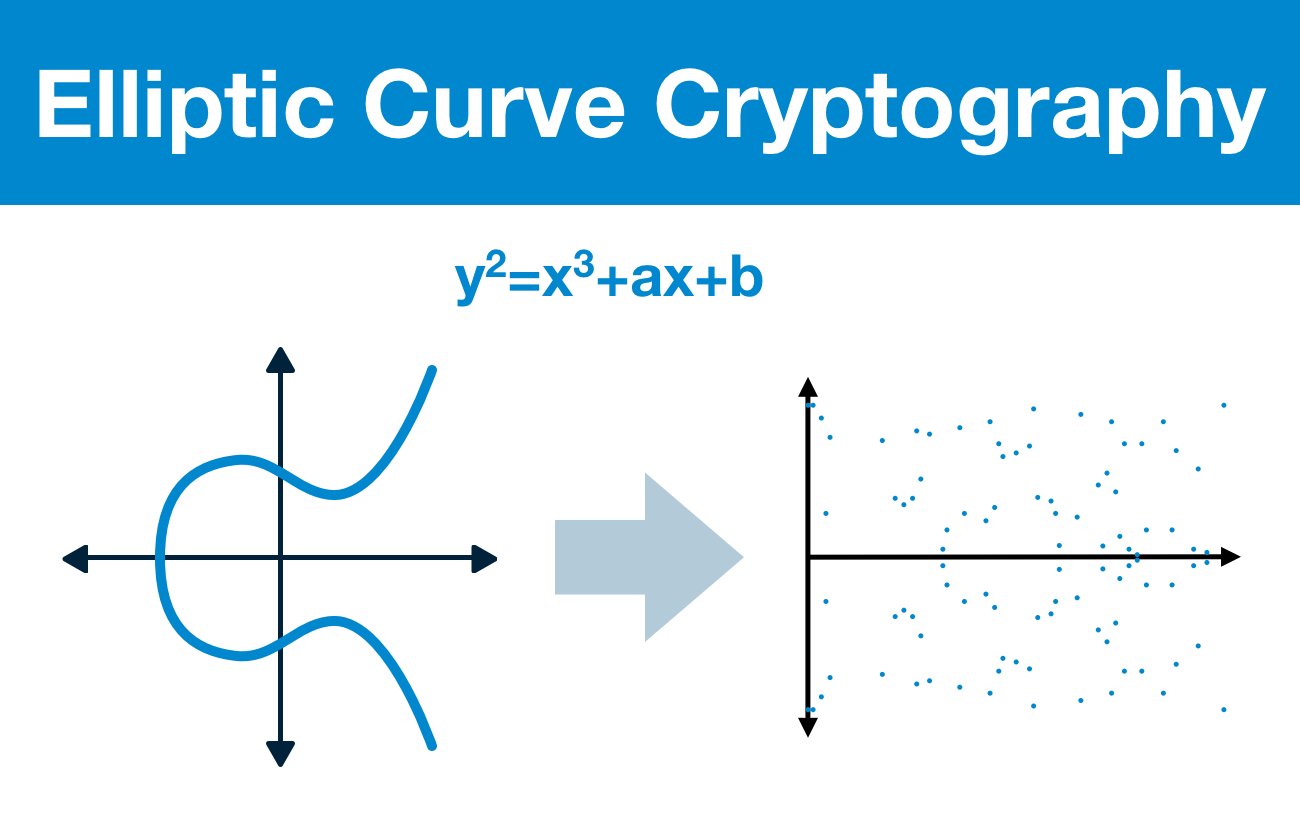
At the core of the elliptic curve concept is a set of cubic equations in two variables. The general form of an elliptic curve can be expressed as y2 = x3 + ax + b, where a and b are constants that determine the specific shape and properties of the curve. The solutions to this equation produce a graph that is symmetric about the x-axis and forms a loop-like structure. However, what makes these curves particularly captivating is not their appearance but their underlying algebraic structure and geometric properties.
One particularly fascinating aspect of elliptic curves is their ability to facilitate complex mathematical operations. The points on these curves, when analyzed with respect to a predetermined addition operation, exhibit group-like behavior. This grouping is crucial because it leads to the ability to define a form of addition between points on the curve, enabling operations crucial for cryptographic protocols.
The Intersection of Algebra and Geometry
Elliptic curves are more than mere abstract mathematical constructs; they merge algebra with geometry, creating a framework where geometric intuition interleaves with number theory. This synthesis allows for easier manipulation of numbers, thus simplifying calculations that are tremendously useful in cryptographic systems.
Consider the importance of the elliptic curve discrete logarithm problem (ECDLP). In simple terms, given a point on an elliptic curve and a multiple of that point, determining the original integer that was multiplied is computationally infeasible. This property forms the bedrock of the security in elliptic curve cryptography (ECC), as it creates a one-way function that is difficult to reverse.
Why Elliptic Curves Matter in Cryptography
Elliptic curves bring several advantages to the table, prompting a significant shift in perspective within the cryptographic community. Foremost among these advantages is efficiency. ECC requires smaller key sizes compared to traditional cryptographic systems, such as RSA, to achieve an equivalent level of security. For instance, a 256-bit key in ECC is considered to be approximately as secure as a 3072-bit RSA key. This compactness allows for faster computations, which is particularly advantageous for resource-constrained devices such as smartphones and IoT gadgets.
Moreover, the robustness of elliptic curves against certain algorithmic attacks enhances their appeal. As computational power advances, so do the tactics employed by adversaries to compromise security systems. ECC’s mathematical underpinnings provide a solid defense, making it an attractive choice for securing both communications and sensitive data.
One striking application of elliptic curves is in the realm of public-key cryptography. Elliptic Curve Diffie-Hellman (ECDH) is a method for secure key exchange over an insecure channel. Through the properties of elliptic curves, two parties can establish a shared secret, which enables encrypted communication without the need for exchanging private keys directly. This peer-based model is not only efficient but also inherently secure, significantly reducing the attack surface.
The Role of Elliptic Curves in Digital Signatures
Another vital application is found in digital signatures, where the authenticity and integrity of messages must be assured. The Elliptic Curve Digital Signature Algorithm (ECDSA) leverages the unique properties of elliptic curves to generate a digital signature that is compact and secure. The process involves selecting a private key from the elliptic curve, which corresponds to a public key that can be disseminated openly. The brief yet potent signatures produced not only save bandwidth but also minimize computational overhead.
Future Outlook: The Evolution of Cryptography
The implications of elliptic curves extend beyond current applications, as advancements in quantum computing pose new threats to traditional cryptographic methods. As researchers explore post-quantum cryptography, elliptic curves may play a pivotal role in developing algorithms resistant to quantum attacks. The flexibility and efficiency of elliptic curve structures make them an ideal candidate for new cryptographic frameworks designed to withstand the impending computational revolution.
In conclusion, elliptic curves encapsulate a fascinating blend of abstract mathematics and practical utility. Their unique properties facilitate advanced cryptographic protocols that promise not only improved efficiency but also a heightened level of security. As the digital landscape continues to evolve, the relevance of elliptic curves in safeguarding data and ensuring secure communication will undoubtedly endure. Embracing these complex yet elegant mathematical entities invites a paradigm shift in our approach to cryptography, challenging us to rethink existing methodologies in the pursuit of enhanced security.






Leave a Comment