In the realm of cryptography, a curious concept arises: associative symmetric encryption algorithms. One might wonder, “Can such algorithms exist?” This playful inquiry cloaks a multifaceted challenge that beckons exploration into the very fabric of encryption techniques.
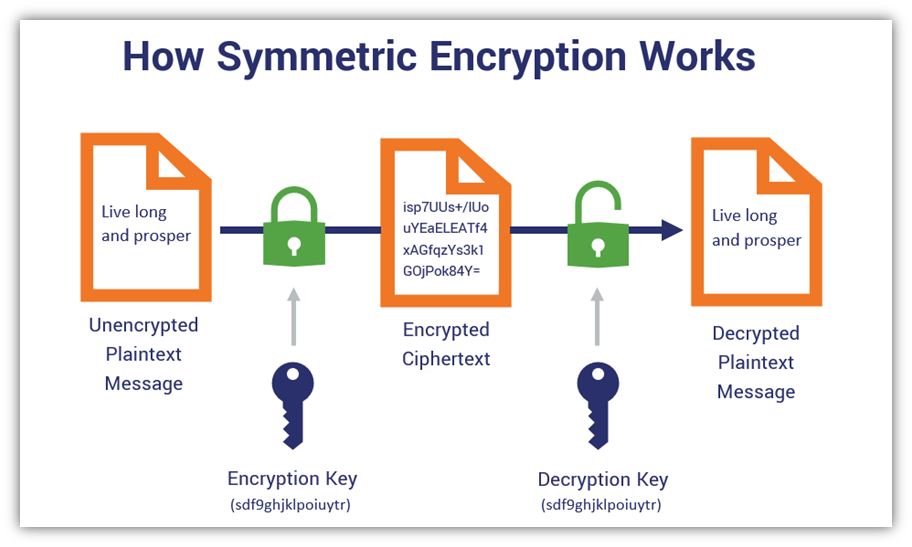
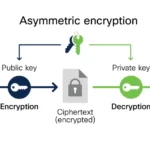
Symmetric encryption underpins much of modern data security. It utilizes a single key for both encryption and decryption, in stark contrast to asymmetric methods that employ pairs of keys. The fundamental principle here relies on confidentiality—ensuring that only authorized parties can access sensitive information. Yet, as one delves deeper, an inherent complexity surfaces when pondering the associative nature of symmetric algorithms. Can encryption operations maintain their associative properties akin to mathematical operations?
To elucidate this notion, one must first grasp the principle of associativity. In mathematics, associativity pertains to the idea that the grouping of operations does not affect the final outcome. For example, in the addition of numbers, (a + b) + c is equivalent to a + (b + c). This raises an enticing question: if we were to encode data symmetrically, could we combine encryption operations without altering the resultant decryption?
To engage with this challenge, let’s consider three fundamental aspects: the definition of associativity in cryptography, the practical implications of such an attribute, and the potential algorithms that might fit this niche.
Firstly, defining associativity in the context of symmetric encryption poses a challenge. Most conventional symmetric algorithms, including AES (Advanced Encryption Standard) and DES (Data Encryption Standard), do not demonstrate associative properties. When one encrypts data multiple times, the resultant output can vary significantly depending on the order of operations. Hence, one must identify whether a symmetric algorithm can yield outcomes analogous to mathematical associativity.
Digging deeper into practical implications, the associations of encryption tasks often come into play during complex data transformations. Imagine a scenario where multiple segments of data require encrypted storage before being concatenated. Non-associative operations might dictate that the resultant encrypted data could differ vastly based on the sequence of encryption—thus complicating the recovery of the original plaintext.
This brings us to the heart of the matter: the quest for associative symmetric encryption algorithms. A potential approach could involve the use of specific mathematical structures such as group theory, where a set equipped with an associative operation exists. One might envision constructing an associative encryption mechanism based on group operations, integrating modular arithmetic, or exploring homomorphic encryption, which allows for computations on ciphertext. However, these approaches demand meticulous deliberation over security ramifications.
For instance, consider the concept of homomorphic properties. Although associated with asymmetric encryption methods, investigating their potential application within symmetric schemes could offer intriguing possibilities. The underlying operations in elliptic curve cryptography demonstrate this principle, exposing an avenue where encryption supports associative-like behavior. However, the complexities of transferring these attributes to symmetric methods could prove daunting.
Moreover, the mathematical properties of various algebraic structures could be harnessed to forge associative encryption techniques. Configuration of new symmetric encryption systems, inspired by lattice-based approaches or other advanced mathematical frameworks, consolidates burgeoning research in this arena. Exploring the capabilities of multivariate polynomials or systems of equations may yield an innovative associative encryption approach. Yet, the challenge remains in navigating security and performance implications inherent in these avant-garde techniques.
A pragmatic glimpse into existing examples of encryption hints at the challenges faced. Many encryption protocols, such as those utilized in secure communication channels (e.g., SSL/TLS), implement a flow of operations that are designed for efficiency and security. These protocols are not merely mathematical exercises—they involve intricate engineering and design choices to safeguard against an ever-evolving spectrum of attacks. Hence, the potential development of an associative symmetric encryption algorithm must duly weigh efficiency and resistance to vulnerabilities.
On the horizon, advancements in quantum computing propel a new dimension of cryptographic discourse, necessitating agility in response to transformative threats. If one were to devise an associative symmetric encryption algorithm, the necessity to fortify against emergent quantum resources amplifies the demand for innovation.
So to the inquisitive mind pondering the existence of associative symmetric encryption algorithms, numerous nuances emerge. The potential for such algorithms does not merely dwell in the realm of theoretical musings. Rather, it embodies a convergence of mathematical elegance, real-world applicability, and enduring security challenges. The road to establishing associative symmetric encryption may be riddled with obstacles; yet, it holds promises for novel constructions that could redefine encryption paradigms.
In conclusion, while the pursuit of associative symmetric encryption algorithms is fraught with complexity and uncertainty, the ensuing dialogue it ignites reveals the dynamism intrinsic to cryptographic research. It calls for continuous innovation and the relentless questioning of established paradigms, ensuring that the quest to secure our data remains as fortified as the technology intended to protect it. As this discourse evolves, the playful question of whether associativity within symmetric encryption can truly manifest beckons us toward further exploration and discovery in the cryptographic cosmos.




Leave a Comment