Imagine a world where complex mathematical concepts unfold like intricate patterns in nature, revealing their elegance and utility in everyday life. If you have ever gazed at the night sky, pondering the mysterious forms of the stars and planets, you may begin to see the parallel between these celestial bodies and the fascinating world of elliptic curves. These curves, often shrouded in abstraction, are not just mathematical curiosities; they are pivotal in modern cryptography, forming the backbone of secure communications across the digital landscape.
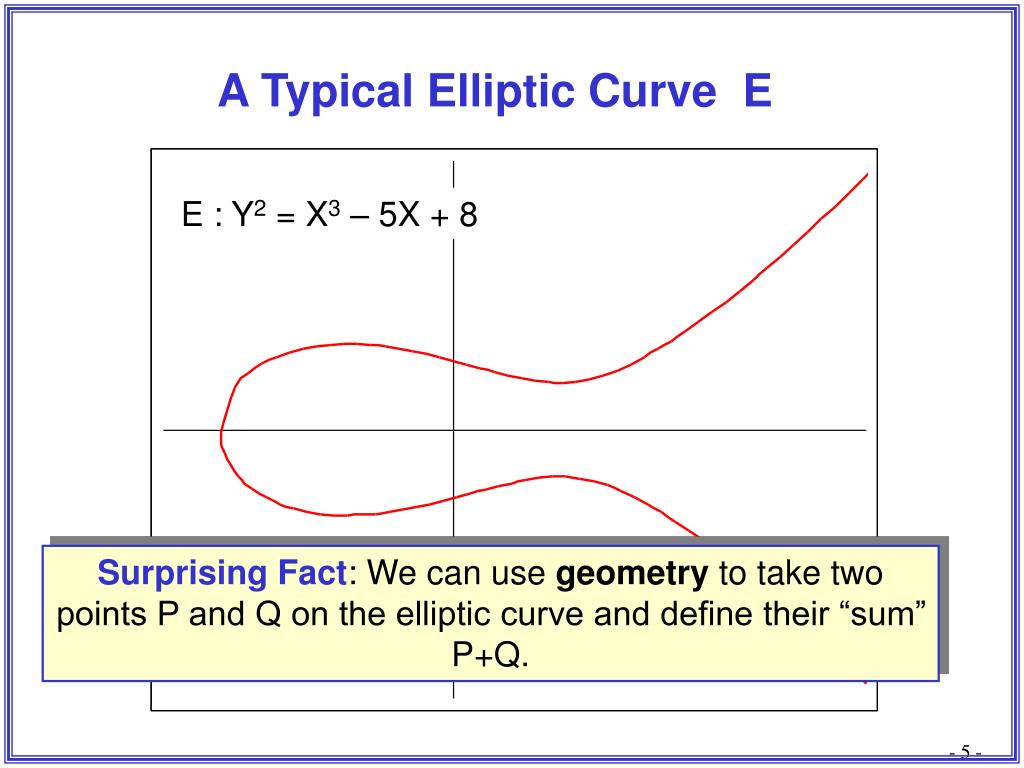
To embark on this journey of understanding, let’s first consider the fundamental definition of an elliptic curve. At its essence, an elliptic curve is a smooth, algebraic curve defined by a specific type of equation. The most commonly referenced form of an elliptic curve is the Weierstrass equation, which is described as y² = x³ + ax + b, where a and b are constants that ensure the curve remains smooth without any sharp points or cusps. These curves possess a symmetrical, beautiful shape resembling a loop, yet they embody profound mathematical significance.
So, why should elliptic curves matter to you? Picture, if you will, a digital treasure chest, securely locked away with a wondrous key whose shape is determined by an elliptic curve. Every time you make an online purchase or send a confidential email, elliptic curves can play an instrumental role in safeguarding your information. But, how exactly do these curves achieve this form of protection? The answer lies in the domain of number theory and the intricacies of elliptic curve cryptography (ECC).
Herein lies a challenge that weaves through the world of mathematics: how do we derive security from something as abstract and seemingly intricate as an elliptic curve? The crux of the matter resides in the notion of a mathematical operation known as point addition. Imagine two points on the elliptic curve, represented as (x₁, y₁) and (x₂, y₂). When we perform this operation using the curve’s geometric properties, we can summon a third point on the same curve, embodying all the mystery and nuance of its construction. The ability to manipulate these points enables the generation of keys used in encryption processes.
An equally intriguing aspect of elliptic curves is their scalability and efficiency when compared to traditional cryptographic systems, such as RSA. While RSA’s security relies on the factorization of large prime numbers—a feat that can become computationally taxing—elliptic curve cryptography harnesses the properties of elliptic curves over finite fields, allowing for shorter keys that yield equivalent security. For example, a 256-bit key in ECC offers a security level akin to a 3072-bit key in RSA. This efficiency means that with elliptic curves, not only is the encryption process swifter, but it also consumes less power, making it ideal for mobile and embedded systems.
Consider, for a moment, the parallels between elliptic curves and music. Just as melodies are composed of notes harmonizing to create a beautiful symphony, elliptic curves consist of numbers and points that interact in a delightful dance, producing complex structures and relationships. This comparison exposes the foundational beauty in mathematics, often hidden beneath layers of abstraction. In revealing such connections, it becomes evident that elliptic curves are instrumental not just in cryptography but also in various other domains such as number theory, algebraic geometry, and even cryptanalysis.
Nevertheless, the allure of elliptic curves and their applications does not come without pitfalls. Security vulnerabilities may emerge from improper implementations or insufficient key sizes. To strengthen their efficacy, researchers are continuously challenged to devise novel algorithms that reinforce the robustness of elliptic curve systems further. As we navigate this labyrinth of complexity, we find ourselves at the forefront of an ongoing investigation, wherein mathematicians and cryptographers alike must remain vigilant to protect against potential threats.
The journey through the realm of elliptic curves casts a dazzling light on how abstract mathematics is interwoven with our everyday experiences. It raises tantalizing questions—such as what additional applications could arise from deeper explorations into these curves? As researchers delve into the uncharted terrain of elliptic curves, the quest for innovative solutions remains insatiable.
In conclusion, the narrative surrounding elliptic curves is one of elegance and pragmatism. These mathematical entities are not merely esoteric phenomena; they possess tangible impacts on the security of our digital interactions. From their unique properties defined by their algebraic equations to their practical applications in cryptography, elliptic curves illustrate the profound connection between mathematics and the modern world. Whether you are a casual observer or an aspiring mathematician, understanding elliptic curves opens a portal into a realm of intellectual exploration, where every question leads only to deeper inquiries, perpetuating an endless quest for knowledge.





Leave a Comment