Elliptic Curve Cryptography, or ECC, might sound like a complex and intricate concept, but when dissected with the right metaphors, it becomes significantly more digestible. In fact, by likening the principles of ECC to simple sandwiches and their delightful curves, we can unravel the mysteries of this sophisticated cryptographic technique. This approach not only simplifies the technical jargon but also emphasizes its unique appeal and functionality. Buckle up as we embark on this culinary journey through the landscape of ECC.
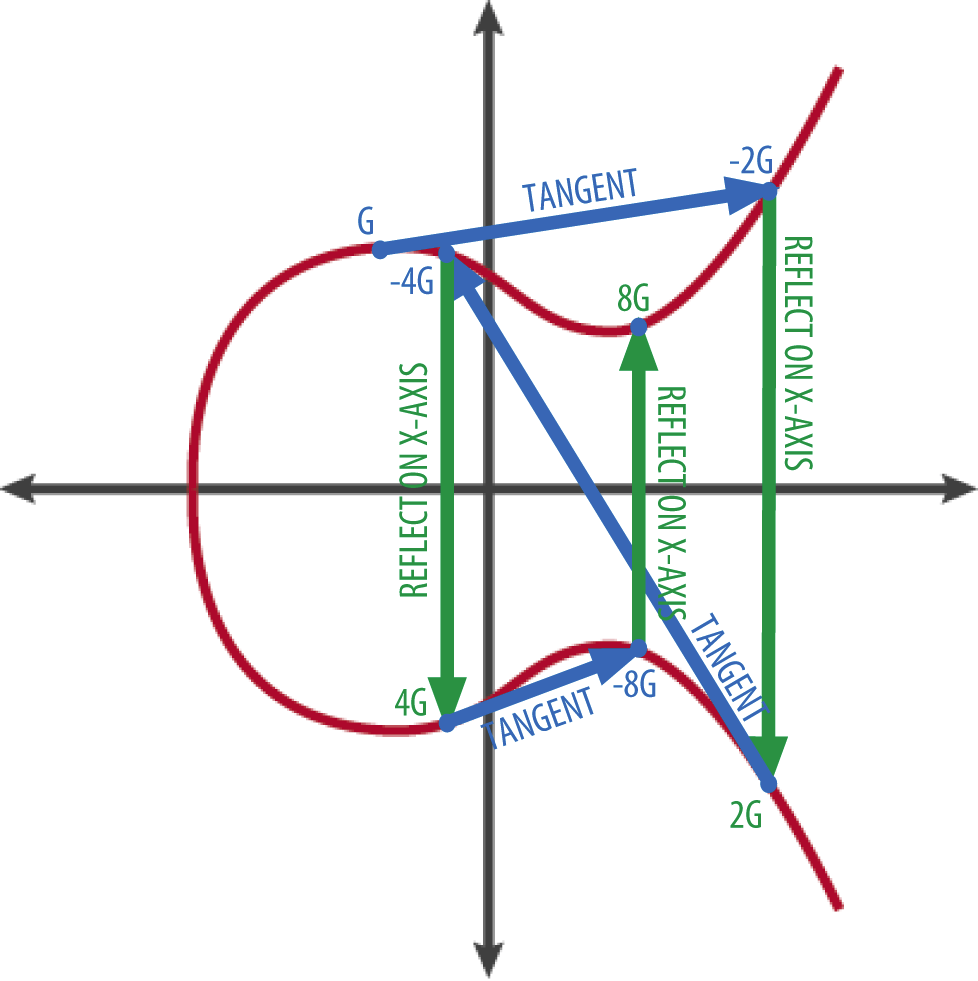
The foundation of ECC lies in the mathematical construct of elliptic curves. These curves can be visualized as flowing, graceful shapes that depict the relationship between variables on a graph. Imagine the gentle arc of a sandwich, where the bread forms a curved, encompassing exterior. Just as the bread supports the fillings, the elliptic curve serves to uphold the key relationships in cryptographic processes. Each point on this curve represents a potential solution to our equations, akin to each ingredient resting comfortably within our carefully crafted sandwich.
To grasp ECC, one must first appreciate the fundamental idea of a key pair — akin to a sandwich recipe shared between two friends. In this case, one friend (the sender) possesses the recipe (the private key) while the other (the recipient) knows how to construct the sandwich using the common ingredients (the public key). The beauty of ECC is that these two elements — the private and public keys — can be connected through the artistic features of our curve.
Now, let’s dive a bit deeper into the sandwich metaphor. Picture a classic club sandwich, stacked meticulously with layers of turkey, lettuce, tomatoes, and bacon. Each layer can be represented by an integer point on the elliptic curve. When two points (or toppings) are combined, they can lead to yet another point, symbolizing a new flavor profile or perhaps a new sandwich variant. This is analogous to the process of point addition in elliptic curves. When adding two points on an elliptic curve, you effectively create a third point, which is also on the curve.
But how do we use this mathematical salad to secure information? Herein lies the elegance of ECC. Just as the combination of various ingredients results in a unique sandwich, the combination of points on the curve can derive a new key. In ECC, this manifests through scalar multiplication, where you scale a point by an integer. The more layers you add — the more intensive the multiplication — the more robust and secure your resulting “sandwich” becomes.
Let’s add some spice to our culinary escapade by introducing the concept of modular arithmetic. This mathematical technique is like deciding how many slices of cheese can fit between the layers of our sandwich without spilling over the edges. In the world of ECC, we confine operations to a certain range to ensure that values do not surpass a defined limit. Thus, just as you might cut a towering sandwich down to manageable sizes, modular arithmetic ensures that calculations stay within the bounds of our elliptic curves.
Delving deeper into cryptographic processes, consider the necessity of securing messages, much like preserving the integrity of a carefully made sandwich. When Alice wants to send a message to Bob, she takes his public key — representing a shared ingredient — and myriads it through the structure of the elliptic curve. Once mixed thoroughly, she generates a shared secret by employing her private key, which is never disclosed. This dual-layer protection echoes the need for keeping certain sandwich ingredients secret while allowing popular ones to be shared freely.
Now, let’s touch on security through complexity. Much like a secret sandwich recipe that promises unique flavors, ECC’s security stems from the difficulty of certain mathematical problems. While the ingredients (or keys) may be publicly accessible, unearthing the private key from the public key is akin to reverse engineering a well-crafted sandwich: ultimately arbitrary and exceptionally challenging. This unique characteristic of ECC makes it highly appealing for secure communications, especially in an age where cyber threats loom large.
Furthermore, as our culinary metaphor progresses, it’s essential to note the efficiency of ECC. Just like a compact sandwich can provide complete satisfaction without overwhelming one’s appetite, ECC allows for smaller key sizes while maintaining robust security compared to traditional cryptographic solutions. This is vital as it results in faster computations and less bandwidth consumption — ideal for a world keen on quick communication.
In conclusion, envisioning ECC through the lens of sandwiches and curves not only simplifies its foundational concepts but also showcases its unique appeal in a practical framework. The graceful arcs and points on elliptic curves serve as reminders of the elegant intricacies present in cryptography. As we navigate through technological advancements, understanding the art of ECC will empower us to appreciate the secure communication that underpins our modern world. So, next time you bite into a delectable sandwich, consider the unseen layers of complexity — much like ECC — that contribute to our sharing of information in profound and secure ways.




Leave a Comment