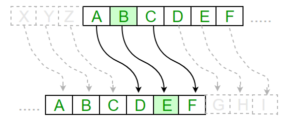
In the realm of cryptography, the substitution cipher stands as a venerable sentinel of secrecy. It is an elegant yet deceptively simple system where each letter in the plaintext is replaced by a letter with some fixed relationship to it. To the untrained eye, it may appear as an insurmountable barrier against prying eyes. However, upon closer examination, one may find that breaking this cipher with brute force resembles the futile attempt of a fledgling bird striving to soar beyond the confines of its cage.
Brute force, in the context of cryptographic attacks, is akin to the lumbering approach of an ancient, rusted machine grinding its gears in an unyielding quest to decipher the unknown. It involves systematically trying every possible key until the correct one is discovered. For a substitution cipher, the analogy holds considerable weight. The vast tableau of possibilities, although seemingly expansive, is ultimately finite. In the case of a simple substitution cipher that operates on the 26 letters of the English alphabet, the number of permutations is capped at 26! (factorial), which equals a staggering 403291461126605635584000000. However, the practical application of brute forcing a substitution cipher is a far more nuanced endeavor.
One of the quintessential weaknesses of a substitution cipher lies in the structure of the language itself. English, for instance, is laden with frequency distribution patterns that can serve as a navigational compass for cryptanalysts. Letters such as ‘E’, ‘T’, and ‘A’ occur with notable regularity in written texts. Consequently, by analyzing the frequency of characters within a ciphered message, one can create a rudimentary map, guiding the mind through the treacherous waters of the encrypted landscape.
The analytical dissection of language affords the cryptanalyst an opportunity to sidestep the relentless machinery of brute force. Instead of blindly pursuing every possible key, one can employ statistical analysis as a weapon. By juxtaposing the frequency of letters in the ciphertext against the known frequencies of letters in the English language, tantalizing clues emerge. For instance, if a character appears an inordinate number of times, it is reasonable to hypothesize that this character might stand in for one of the commonly used letters such as ‘E’ or ‘T’. Thus, the cipher unveils itself like an unfurling flower, revealing its underlying beauty.
Furthermore, the intricate tapestry of digrams and trigrams—combinations of two or three letters—offers another layer of insight. Familiarities abound in the English language: the prevalence of ‘th’, ‘he’, ‘in’, and ‘er’ can be exploited to formulate educated guesses regarding the cipher’s mapping. The rumors of its failure can be exaggerated, as many real-world applications have witnessed the demise of substitution ciphers to linguistic prowess. This is why the seemingly simple substitution cipher becomes a perennial challenge: it dances precariously between simplicity and complexity.
To further complicate matters, variations of the substitution cipher, such as the homophonic substitution cipher, deliberately obfuscate frequency patterns by allowing each letter to map to multiple symbols. Such designs can indeed baffle brute force methods, as they introduce an additional layer of complexity that requires more than mere frequency analysis to decipher. Yet, even in these convolutions, the resolute analyst finds openings, employing advanced techniques like pattern recognition and ciphertext clustering to chip away at the disguised façade.
In cryptography, a notable axiom is that no cipher is unbreakable; rather, it exists in a state of equilibrium where it can be broken by the right talent and enough time. Enter the notion of computational advancements in the digital age. Brute force techniques, bolstered by the unfathomable power of modern computers, can test potential keys at an unprecedented speed. However, even in this landscape, the advantages of linguistic analysis remain paramount. The true strength of substitution ciphers diminishes when faced with enlightened approaches that marry statistical analysis with computational might.
As cryptographers and cryptanalysts engage in their cerebral duel, the substitution cipher emerges as a microcosm of a larger battle: the perennial struggle between secrecy and revelation, obscurity and clarity. With every breakthrough against such ciphers, the art of cryptography continues to evolve. Sophisticated forms like polygraphic ciphers and modern encryption algorithms wield far greater complexity than their predecessors. Yet, the roots of cryptography remain intertwined with these early rudimentary forms, reminding us of their significance.
In conclusion, can one truly break a substitution cipher using brute force? The answer is a nuanced ‘yes,’ but with caveats. While brute force remains a tool in one’s arsenal, the key to unlocking this cipher often lies not in sheer numbers, but in understanding, observation, and intuition. The mathematical grandeur of the permutations may captivate the imagination, but it is the subtleties of language that eventually guide one towards clarity and understanding. Hence, we are left with a metaphor: breaking a substitution cipher is less about bulldozing through walls and more akin to deftly picking the lock, revealing the secrets that lie beyond with elegance and ease.





Leave a Comment