In the intricate realm of cryptography, one might presume that mathematical constants and transcendental numbers hold little sway over the esoteric codes safeguarding our digital communications. However, the enigmatic constant π (Pi) emerges as an unexpected contender in this complex field. As we delve into this mathematical wonder, the implications of its properties may well reshape our understanding of cryptographic methods.
The significance of π extends beyond mere geometry. Defined as the ratio of a circle’s circumference to its diameter, π is an irrational number possessing a decimal expansion that continues indefinitely without repetition. This property alone lends π an intriguing character, suggesting an infinite array of digits that could potentially serve diverse functions in cryptographic systems. Yet, it is the structural and probabilistic properties of π that merit profound consideration.
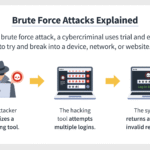
To appreciate π’s role in cryptography, one must first consider the foundational principles that govern the field. Cryptography relies heavily on algorithms and protocols designed to secure communication and protect sensitive information. Within these frameworks, randomness is paramount. High-quality randomness is critical for generating keys, ensuring that they are sufficiently unpredictable, which is crucial for thwarting potential adversaries.
Herein lies the crux of π’s contribution: its digits have been extensively studied for their statistical properties, leading to the assertion that they exhibit apparent normality. In probability theory, a number is termed normal if, in its infinite decimal expansion, each digit appears with equal frequency, and all combinations of digits occur with the expected frequency. This statistical behavior renders π a candidate for randomness, which cryptographers can leverage in algorithmic applications.
Take, for instance, the construction of pseudo-random number generators (PRNGs), a cornerstone of modern cryptographic protocols. PRNGs generate sequences of numbers that approximate the properties of random numbers. The challenge lies in ensuring that these sequences remain unpredictable and, therefore, secure. By integrating digits of π into the seed values of such generators, cryptographers can harness its seemingly chaotic nature to enhance randomness.
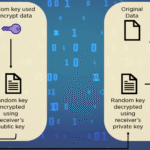
Furthermore, the utilization of π in cryptography transcends mere random number generation. Its role extends to the formulation of hash functions, which are pivotal in preserving data integrity and authentication. Hash functions take input data and transform it into a fixed-size string of characters, which is unique to each input. The robustness of these functions relies on their sensitivity to changes in input; a minute alteration should provoke a drastically different output, deterring attackers from manipulating the underlying data.
In this context, π’s digits can be employed as constants in hash function algorithms. The unpredictability of π, coupled with the uniform distribution of its digits, contributes to creating hash functions that are less susceptible to collisions—instances where two different inputs yield the same hash output. Such properties are indispensable in devising secure hash algorithms, vital for blockchains and digital signatures.
Another notable area where π finds relevance is in public key cryptography, specifically within algorithms such as RSA and ECC (Elliptic Curve Cryptography). Both RSA and ECC hinge on the complexity of certain mathematical problems, which serve as the foundation for key generation and encryption. While π may not play a direct role in these algorithms, the underlying structures exhibit fascinating parallels to the mathematical theories that define π itself.
The curves defined by elliptic functions, for instance, can echo the nuanced behaviors of π within certain theoretical frameworks. This harmony between geometrical constructs and cryptographic algorithms fosters novel avenues for research, potentially leading to enhanced security protocols that exploit the intrinsic properties of these mathematical concepts.
Moreover, an intriguing application of π is its inclusion in steganography—the art of concealing messages within other, seemingly innocuous data. Encrypted information can be cleverly embedded within digit sequences derived from π, allowing for discreet communication avenues. The seemingly random nature of π’s digits provides an ideal cover, complicating adversarial attempts to discern hidden messages. The creative fusion of number theory and data concealment exemplifies how cryptographic methodologies can adapt and innovate over time.
Despite the promise that π offers to the field of cryptography, it is crucial to maintain a discerning perspective. The quest for true randomness remains an ever-fleeting endeavor, with mathematicians and cryptographers continuously exploring new frontiers. Although π provides tantalizing hints of promise, the need for robust security mechanisms persists, ensuring that digital communications remain fortified against increasingly sophisticated threats.
In conclusion, the mathematical constant π has indeed found an unexpected niche within the cryptographic landscape, proving that the boundaries of this field are as expansive as the concept of infinity itself. By examining its properties and exploring innovative applications, cryptocurrency enthusiasts and security experts alike can gain new insights into the structuring of secure communications. As the digital world continues to evolve, the integration of such constants into cryptographic practices will undoubtedly spur further curiosity and exploration, reminding us that even the most familiar elements of mathematics can harbor surprising complexities and potential.






Leave a Comment