When we consider the vast landscape of modern cryptography, elliptic curve cryptography (ECC) emerges as a powerful player, much like a petite yet agile felon in the intricate world of document security. What makes ECC so compelling? Imagine for a moment that cryptography is a fortress, where each locking mechanism serves as a bulwark against unauthorized access. ECC offers a nimble yet formidable gatekeeper, enabling secure communications with relatively small keys, unlike its more cumbersome counterparts.
To understand the profound implications of ECC, one must first grasp the underlying mathematics. At the heart of ECC is the mathematical structure known as an elliptic curve, which is defined by an equation of the form y² = x³ + ax + b. Each point on this curve can be visualized as a location on a smooth, rolling landscape, where the properties of the curve lend themselves to cryptographic purposes. These curves exhibit fascinating properties, including a rich group structure that allows for efficient computations essential for encryption and decryption processes.
Picture this: You’re hiking up a spectacular mountain trail. This mountain symbolizes the elliptic curve, and the peaks represent the points on that curve. The higher you climb, the more secure your position becomes. Just as reaching the summit allows you a sweeping view of the surrounding terrain, navigating the mathematical complexities of ECC provides an insight into the robust security it offers. At this impressive elevation, even the smallest changes can have vast repercussions; such is the case with elliptic curves. A minor tweak in parameters can lead to a substantial increase in operational security.
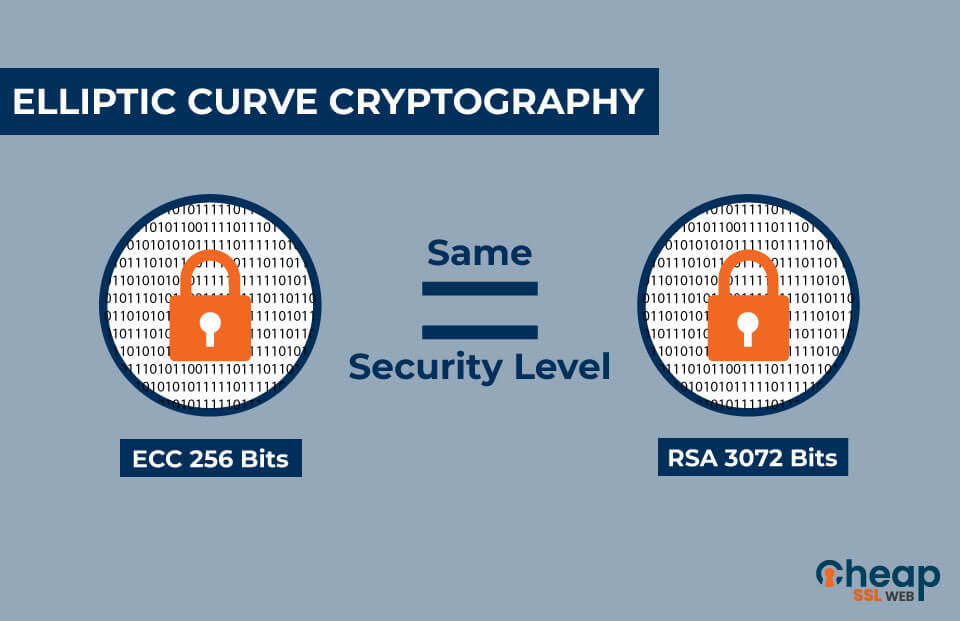
Now, let’s introduce a playful challenge: What if you had to design a lock for your digital information that is impervious to any would-be thief? The existing locks—like RSA or DSA—are akin to enormous vault doors, impressive yet cumbersome. On the other hand, ECC is akin to an intricate, beautifully designed puzzle box, compact in size but intricate in design. It manages to achieve comparable, if not superior, security levels with significantly smaller key sizes, resulting in faster computations and less power consumption.
A key component of ECC revolves around something known as the ‘discrete logarithm problem’. This concept is fundamental in understanding why ECC can maintain security even with smaller keys. To illustrate, consider a game of hide and seek, where you and your friend hide behind trees on the mountain. If you can easily identify your friend’s hiding spot without ambiguity, then the game is compromised. In the world of ECC, the ‘discrete logarithm problem’ is the challenge that ensures the rightful player retains the ability to hide effectively: though the position may be known, calculating the original hiding place remains elusive.
Visually, one might imagine the elliptic curve as a dramatic ocean wave, continuously undulating and flowing. As you traverse the crest, you see that each point on the wave interacts with the next, echoing the complex relationship between keys in ECC. A powerful wave might drag you into its embrace, yet at the same time, these curves present a method for maintaining a balance between strength and accessibility—a dance between risk and security.
But why opt for ECC over traditional cryptography? The answer lies in efficiency. In the realm of mobile computing, where resources and power are limited, ECC presents itself as a goldmine for developers and users alike. It offers enhanced security without taxing the system’s performance. This is akin to favoring a light yet sturdy backpack for your mountain expedition rather than burdening yourself with excess weight. Light yet effective equipment makes for a more enjoyable and successful journey.
This leads us to the haunting specter of the quantum computing revolution. As we stand at the brink of this formidable advancement, the efficacy of traditionally strong cryptographic methods faces unprecedented challenges. In this new world, ECC stands potentially more resilient. If we liken quantum computing to a colossal storm barreling towards our serene landscape, ECC emerges as perhaps the most adaptable construct, ready to navigate the tempest with minimal disruption.
Envision the future of secure communications under a hybrid cloud of elliptic curve algorithms, gracefully dancing like figures in a ballet. The dance of cryptography must adapt to the rhythms of newer technologies while maintaining the poise necessary to protect our sensitive information. Here, ECC illustrates adaptability—its small footprint makes it an excellent candidate for future-proofing privacy.
Yet, with all of its robust features, ECC is not immune to scrutiny or potential pitfalls. The choice of elliptic curves is critical; poorly chosen curves can compromise the integrity of the system. Just as a hiker must select the right trail to avoid treacherous terrains, cryptographic engineers must judiciously evaluate curve parameters. Recognizing reputable curves becomes paramount in fortifying against vulnerabilities, ensuring that the elegance of defense does not lead to unintentional exposure.
The question now stands: Are we prepared to embrace the challenges and nuances of elliptic curve cryptography? As cyberspace continues to evolve, aligning security measures with current technology is not merely advisable—it is essential. ECC offers a blossoming garden of opportunities within the convoluted patchwork of cryptography, providing not just locks but entire systems capable of safeguarding our digital realities.
In conclusion, the elucidation of elliptic curve cryptography serves as an invitation—a siren call to rethink and realign our approaches to secure communication. ECC promises the agility of a feather in a storm, gracefully threading the needle of security and efficiency. In this adventure of cryptography, the pivotal question emerges: Will we choose the path of traditional locks, or shall we dare to embrace the wonders that elliptic curves can unveil?




Leave a Comment