In the realm of cryptography, RSA (Rivest-Shamir-Adleman) stands as a cornerstone of public-key infrastructure. For many, it serves as an enigmatic entity, a blend of mathematics and security that holds significant importance in safeguarding digital communications. One of the most critical questions surrounding RSA revolves around the relationship between public and private keys: Can a public key unveil its private twin in RSA? This inquiry beckons a deep dive into the mechanics of RSA, its mathematical foundation, and the security assumptions that bolster its effectiveness.
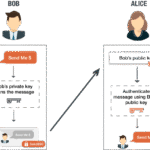
The RSA algorithm primarily relies on the difficulty of factoring large prime numbers. To understand the duality of keys, we must first recognize how they are generated. An RSA key pair is created by selecting two large prime numbers, typically denoted as (p) and (q). The product of these primes, (n = p times q), forms part of the public key. The public key, represented as a pair ((n, e)), where (e) is a chosen exponent that is coprime to (varphi(n)) (Euler’s totient function), is openly shared with all parties who wish to communicate securely.
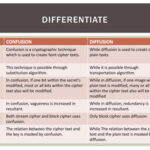
The private key, on the other hand, designed to remain secret, is calculated using the modular multiplicative inverse of (e) modulo (varphi(n)). Hence, it is represented as ((n, d)), where (d) fulfills the equation (d cdot e equiv 1 mod varphi(n)). Given this intricate process, one might wonder: can the public key alone provide enough information to derive the private key?
The straightforward answer, under the current knowledge and computational capabilities, is no. RSA’s security is predicated on the computational infeasibility of factoring the large number (n) into its constituent primes (p) and (q). The sheer size of the numbers involved, typically several hundred digits long, makes it practically impossible for modern computing technology to factor them within a reasonable timeframe. Therefore, the public key does not inherently disclose the private key.
However, this raises an intriguing proposition. What if an adversary possessed significant computational power or advanced algorithms that could bridge the gap between public and private keys? In theory, such a scenario would necessitate a groundbreaking development in number theory or computational techniques. Concepts like Shor’s Algorithm, which exploits quantum computing, could render current RSA implementations obsolete by dramatically reducing the time required to factor large composite numbers.
The intriguing possibility of a public key leading to its private counterpart hinges on the resilience of RSA against various attack vectors. In particular, there exist cryptographic vulnerabilities, although minimal in the context of RSA’s security. For instance, common pitfalls such as poor key generation practices, inadequate key lengths, or reliance on small prime numbers could expose even strong cryptosystems to exploitation. This highlights that while the public key does not directly reveal the private key, systemic flaws or human errors might inadvertently open doors that were thought securely closed.
A deeper examination delves into side-channel attacks, where an adversary leverages information gleaned from the physical implementation of the algorithm rather than the mathematical prowess required to factor (n). Timing attacks, for instance, analyze how long a decryption operation takes based on the private key employed. If the time discrepancies are measurable and significant enough, it may allow an attacker to infer bits of the private key incrementally. Such attacks underscore the importance of robust implementation practices in mitigating vulnerabilities associated with key exposure.
Additionally, consider the role of padding schemes in RSA. Techniques like OAEP (Optimal Asymmetric Encryption Padding) introduce layers of complexity and randomness, thereby reducing the risk of deterministic output from the same plaintext. This is crucial because without proper padding, patterns in the plaintext could potentially lead an adversary closer to deciphering the private key.
Beyond the technicalities, philosophical implications arise from the query: what does it mean for a public key to reveal its private counterpart? This tension between transparency and secrecy reflects broader societal dynamics in digital communications, emphasizing the necessity of trust in the mechanisms underpinning secure interactions.
In conclusion, while the RSA algorithm operates on sound mathematical principles that currently preclude the public key from disclosing its private twin, the landscape of cryptography is perpetually evolving. New theoretical advancements, computational breakthroughs, and pragmatic vulnerabilities necessitate a vigilant approach towards understanding and optimizing cryptographic implementations. The playful inquiry into whether a public key can reveal its private twin is not just a mere mathematical exercise; it embodies a cautionary ethos for the future of secure communications in an increasingly interconnected world.





Leave a Comment