In today’s digital landscape, ensuring data security is paramount. Traditional cryptographic methods, while still prevalent, are gradually being overshadowed by a more sophisticated approach known as Elliptic Curve Cryptography (ECC). This intricate form of encryption utilizes the mathematical properties of elliptic curves to provide robust security, making it increasingly favored for various applications ranging from secure communications to blockchain technology.
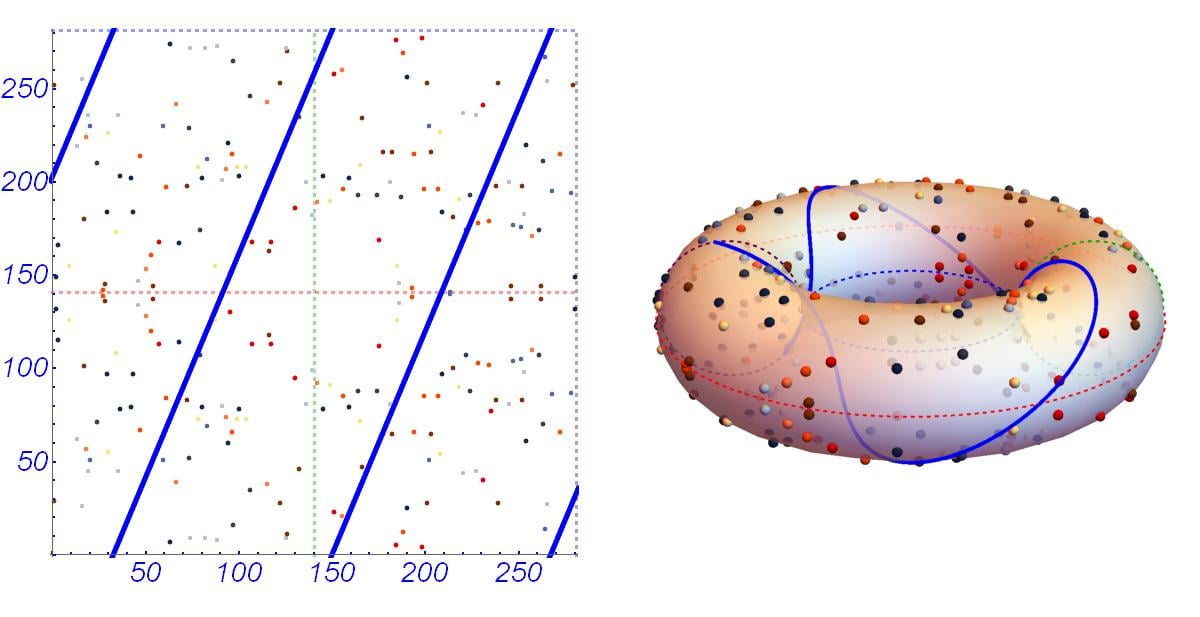
Elliptic curves are defined by equations of the form y² = x³ + ax + b, where the coefficients a and b are integers that lead to a non-singular curve. Unlike classical algorithms, which often rely on the computational difficulty of factoring large numbers or computing discrete logarithms, ECC is based on the hardness of the elliptic curve discrete logarithm problem (ECDLP). This difference in foundation is not merely academic; it allows ECC to achieve the same level of security as traditional systems like RSA with significantly shorter key lengths.
Key lengths are critical in cryptography as they directly influence the computational resources required for attacks. For instance, a 256-bit key in ECC can offer equivalent security to a 3072-bit key in RSA. This disparity means that ECC not only allows for enhanced security measures but also promotes efficiency, reducing the processing power and memory required for encryption and decryption processes. Given the proliferation of mobile devices and the Internet of Things (IoT), where resources are often constrained, the efficiency of ECC makes it highly attractive.
One of the key advantages of ECC is its scalability. As the demand for more secure cryptographic solutions grows, especially with the emergence of quantum computing threatening traditional algorithms, ECC stands poised to address these challenges. While current quantum algorithms can efficiently break many classical encryption methods, ECC remains resilient against such attacks, especially when combined with post-quantum cryptographic techniques.
Practical applications of ECC abound. This form of cryptography is employed in secure sockets layer (SSL) certificates to safeguard internet transactions. When you visit a website that starts with HTTPS, ECC plays a vital role in establishing a secure connection between the web server and the browser. The initial handshake process involves exchanging keys, and ECC allows for the rapid generation of shared secrets, thus ensuring the privacy of data in transit.
Another emerging field utilizing ECC is blockchain technology. Cryptocurrencies such as Bitcoin and Ethereum rely on cryptographic techniques to secure transactions and validate user identities. Here, ECC is instrumental in creating digital signatures which authenticate that a transaction has indeed been authorized by the owner of a private key. This not only bolsters security against fraud but also preserves the integrity of transaction records within the blockchain.
Furthermore, ECC has shown promise in the realm of mobile communications. With the dramatic increase in data traffic across mobile networks, applying cryptographic measures that impose minimal overhead is critical. By utilizing ECC, mobile applications can provide secure messaging services and authenticated user interactions with reduced bandwidth consumption. This efficiency does not compromise on security, ensuring that users are provided with robust protections against potential threats.
In the context of IoT, where myriad devices are interconnected, the lightweight nature of ECC is particularly beneficial. Devices like smart thermostats, wearable fitness trackers, or home automation systems have limited computational capacity. Employing ECC allows these devices to encrypt and transmit data securely without draining their batteries or overloading their processors. The combination of practicality and security epitomizes the transformative potential of elliptic curve technology in the evolving digital ecosystem.
Moreover, several popular cryptographic protocols integrate ECC. Transport Layer Security (TLS), used in browsing and email systems to ensure confidentiality and integrity, has adopted ECC in its newer iterations. In addition, the Advanced Message Authentication Code (CMAC) makes use of ECC concepts to verify the authenticity of messages, enhancing secure communications.
Still, despite its advantages, ECC is not devoid of challenges. Implementing elliptic curves requires a deep understanding of mathematical principles to select appropriate curves and parameters, which can be a deterrent for some developers. Ensuring that these systems are resistant not just to classical threats but also to quantum attacks necessitates ongoing research and enhancement of existing protocols.
As with any technology, the future applicability of ECC depends on the collective efforts of the cryptographic community. As theories mature and new advancements emerge, ECC stands as a cornerstone in securing an increasingly complex digital world. The advancements in elliptic curve algorithms and the dissemination of knowledge regarding their implementation will determine the extent to which they can be trusted as the primary mechanism for securing sensitive information.
In conclusion, elliptic curve cryptography serves not just as an alternative to conventional cryptographic methods – it is a revolutionary advancement that enhances security while mitigating resource consumption. Its application across various sectors highlights its versatility. As the digital world continues to evolve, ECC’s role will undoubtedly expand, heralding a new paradigm in the realm of cryptography.





Leave a Comment